Metrology

The fundamental difference between Vernier calliper and micrometre

Vernier calliper and micrometre are very common to be used for dimensional measurement. However, many people do not know their fundamental difference.

Wahyudin Syam

• 3 min read
The fundamental difference between Vernier calliper and micrometre

Vernier calliper and micrometre are very common to be used for dimensional measurement. Most people know how to use callipers and micrometre. However, many of them do not know the philosophical difference between Vernier calliper and micrometre.

Vernier calliper

The Initial development of Vernier calliper was due to the invention of scale system for resolution amplification by Pierre Vernier in 1631. Then two centuries later, Joseph Brown, an American engineer, developed the scale system into what we know Vernier Calliper.

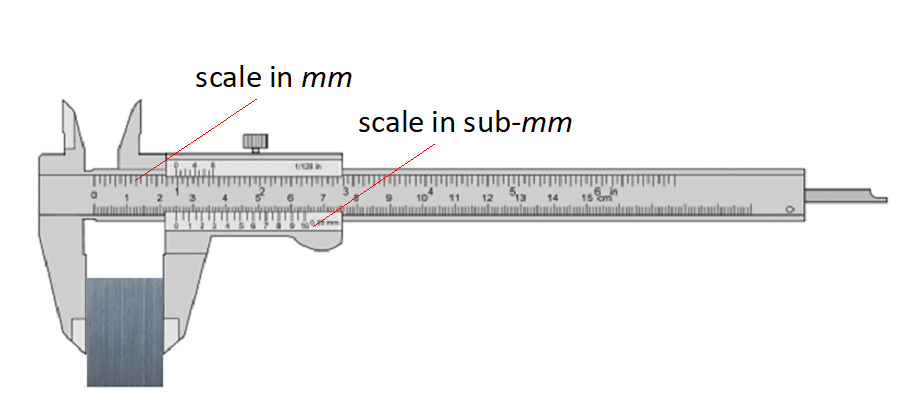
The characteristics of Vernier calliper are (figure 1):

  • It has two types of scale: $mm$ scale with $1 mm$ resolution and $sub-mm scale$ (Vernier scale). The sub-mm scale is commonly from $0.05mm (50\mu m)$ to $0.01mm (10\mu m)$
  • It is an end standard (there are two opposite but parallel sides for measuring)
  • It has several reading-scale types: with manual scale, digital and dial gauge. Callipers with dial-gauge reading have the highest resolution compared to other types
Figure 1: An example of Vernier calliper with two scales: $mm$ scale and sub$-mm$ scale.

Micrometre

Micrometre was invented by William Gascoigne in the 17thcentury (in Yorkshire, England) and is a screw-based measuring instrument. The first commercialisation of micrometre was done by Brown and Shape in 1867.

The characteristics of micrometre are (figure 2):

  • Commonly, it has resolution from $2\mu m$ to $10\mu m$ obtained from screw mechanism.
  • It has main (rough) resolution of $1mm$
  • It is an end standard (there are two opposite but parallel sides for measuring)
  • Like Vernier calliper, it has several reading-scale types: with manual scale, digital and dial gauge. Callipers with dial-gauge reading have the highest resolution compared to other types
Figure 2: An example of micrometre with two scales $mm$ and $\mu m$.

The fundamental difference

Micrometre has higher accuracy than Vernier calliper. The high accuracy of micrometre is not mainly due to higher resolution than calliper. But, there is a fundamental difference of why micrometre has higher accuracy than calliper.

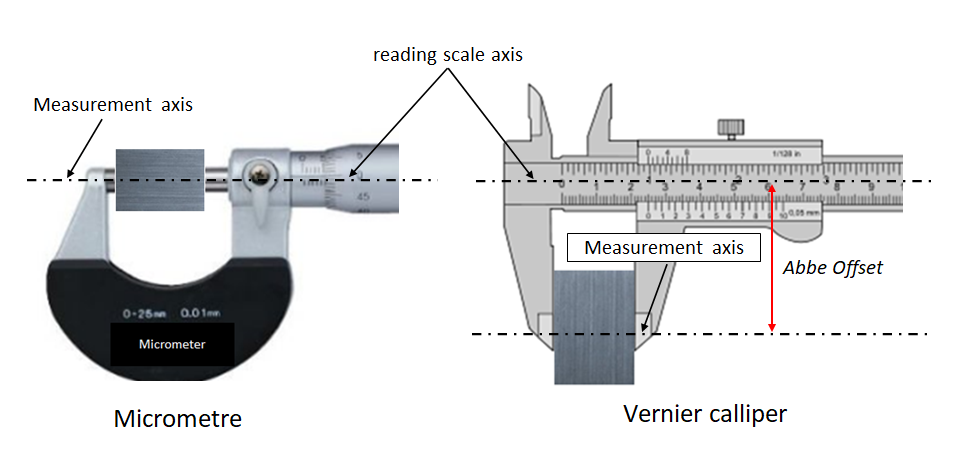
The fundamental difference between micrometre and Vernier calliper is on the basic configuration of their measurement and reading-scale axes.

Micrometre has coaxial measurement axis and reading scale axis. These coaxial axes cause that there is no Abbe offset in their structure (figure 3). Meanwhile, in figure 3, Vernier calliper has measurement and reading scale axes that are not coaxial. Instead, they are offset with a certain distance. Due to non-coaxial axes, there is Abbe offset, leading to Abbe error, on the structure of Vernier calliper.

Abbe offset is the distance between the measurement and reading scale axis of a measuring instrument. This Abbe offset is one of the first principle to comply in the design of measuring instruments.

Abbe offset will cause a certain displacement error when measuring the measurement and reading scale are not parallel to each other. This error is due to that, in reality, there will always imperfection in manufacturing and assembly that cause the two axes are not coaxial each other. Non-parallel measurement and reading scale axes cause a small displacement error when reading a measurement on the reading scale.

Figure 3: The location of the measurement and reading scale axes for micrometre (left) and Vernier calliper (right).

Conclusion

The fundamental difference between Vernier calliper and micrometre is on the Abbe offset on their structural design. In perfect condition, micrometre does not have Abbe offset (despite in reality, due to manufacturing and assembly error, there will be a very small Abbe offset) while Vernier calliper does have Abbe offset. This virtually zero Abbe offset that makes micrometre has higher accuracy than micrometre.

We sell all the source files, EXE file, include and LIB files as well as documentation of ellipse fitting by using C/C++, Qt framework, Eigen and OpenCV libraries in this link.

We sell tutorials (containing PDF files, MATLAB scripts and CAD files) about 3D tolerance stack-up analysis based on statistical method (Monte-Carlo/MC Simulation).