The problematic aspect of number crunching in programming: Case study in GNSS calculations
In programming, especially for languages requiring explicit data type declarations, such as C/C++, FORTRAN and Java, the number of bits to represent numbers are very important.

In programming, especially for languages requiring explicit data type declarations, such as C/C++, FORTRAN and Java, the number of bits to represent numbers are very important.
Processing these numbers (crunching numbers) in scientific and engineering computations, such as GNSS signal processing, are essential for deep understandings of phenomena of interest.
A wrong data type, and hence wrong bit representations, of these numbers will lead to wrong calculation results. These wrong calculation results are then cause wrong understanding and analysis of the phenomena.
Correct data types (and so the number of bits) of variable are fundamental in programming, especially for scientific and engineering calculations that heavily crunch numbers.
We should not overlook this data type.
The importance of the amount of bits to represent numbers in programming
To select a correct data type to use for a variable in programming, we should look at how many decimal digits that a variable will present or contain.
For example, if we have a variable $s$ to represent speed. Let’s say, $s=25.46$. This number has 4 decimal digits (independent whether the value is integer or real).
Since we have 4 decimal digits, then the number of bits to represent the number above is at least 14 bits.
From where we know that we need at least 14 bits?
So, to calculate how many decimal digits $D$ that binary bits can represent, we need to follow the following formula:
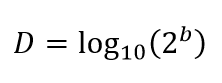
Where $D$ is the number of decimal digits we can get given the number of binary bit availability and $b$ is the number of binary bits used to represent numbers.
So, by using the example above that says we need to have at least 14 bits, we can calculate how many decimal digits $D$ a variable can represent with 14 bits:
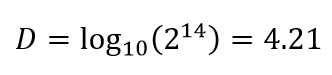
Hence, with 14 bits, we can represent around 4.2 bits decimal digits. Usually we round it so that we can say that with 14 bits, we can represent a number up to 4 decimal digits.
Examples of data type logic error in programming
In programming, one of the hardest mistake to debug is run time errors due to the incorrect use of data type to represent a variable.
Perhaps, in some language that automatically determine the data type of variables, such as MATLAB, this error is not that relevant.
But, for languages that requires explicit data type determinations, this error due to incorrect assignment of data type is very relevant and has significant impacts on the quality of the program and the productivity of the programming activities.
This mistake will cause our calculation results to be completely deviate from what we expect theoretically and is at the same time difficult to find and debug.
Let us have some real examples in C/C++ of this data type logic mistake.
Example 1: wrong use of data type for index of arrays in C/C++
In this example, let say we want to represent the index of an array with a variable $counter$.
When the array has size of 200 elements:
Float data_array[200];
And then we want to represent the index variable as:
int8_t counter = 0;
when we refer the index of the data array inside a loop with 200 iterations as:
for(counter=0;counter<200;counter++){
data_array[counter]= 5;
}
Hence, there will be a runtime error and most likely, the error will not stop the program, instead, we do not insert correctly the data into the $data\_array$ variable. This situation is, very often, difficult to spot or debug.
The reason of this logic error at runtime is that $int8\_ t$ is only 8-bits to present signed integer value.
The last bit is reserved for sign. Hence, only 7-bits are available for integer numbers.
Maximum positive values we can get with 7-bits is only $2^{7}-1=127$, if the index is $200$ that is $> 127$.
Then, when we do a looping to 200 iterations to fill the $data\_array$, at the iterations 128 and so on, the $counter$ variable cannot take the correct value.
This situation causes the $data\_array[counter]$ cannot fill the value into its correct array position, resulting conditions where we do not have the correct values for further processing inside the $data\_array$ variable.
To solve this issue, we can simply change the data type from $int8\_t$ to $uint8\_t$.
This $uint8\_t$ is unsigned integer. Hence we have the full 8 bits to represent positive values up to $2^{8}-1=255$. This $255$ is $> 200$ that is the size of the $data\_array$.
Example 2: wrong use of data type for loop variables in C/C++
Another example of logic error due to wrong data type is on the variable of a loop.
Let say, we want to do a loop for 300 times. Hence, we assign a variable as the counter of the loop as:
int DATA_RATE=300;
for (uint8_t ii = 0; ii < DATA_RATE; ii++) {
…
}
In the code snippet above, the variable $ii$ is declared as $uint8\_t$. Hence, the maximum positive value that the variable $ii$ can contain is $2^{8}-1=255$.
Meanwhile, the $DATA\_RATE$ is defined with a value of 300. In this condition, the condition of $ ii < DATA\_RATE $ is always true so that the loop becomes infinite.
To solve this problem, we can set the data type of $ii$ to data type that can contain more value, such as $uint16\_t$ or $int$.
Case study of numbers in GNSS
A question can be risen, how to estimate that an engineering or scientific calculation require high number of bits?
One way to estimate how large the number of bits will be for a variable is by understanding the unit of the variable and their precision.
In short, we can compare the range of a measured value vs its unit of precision.
For example:
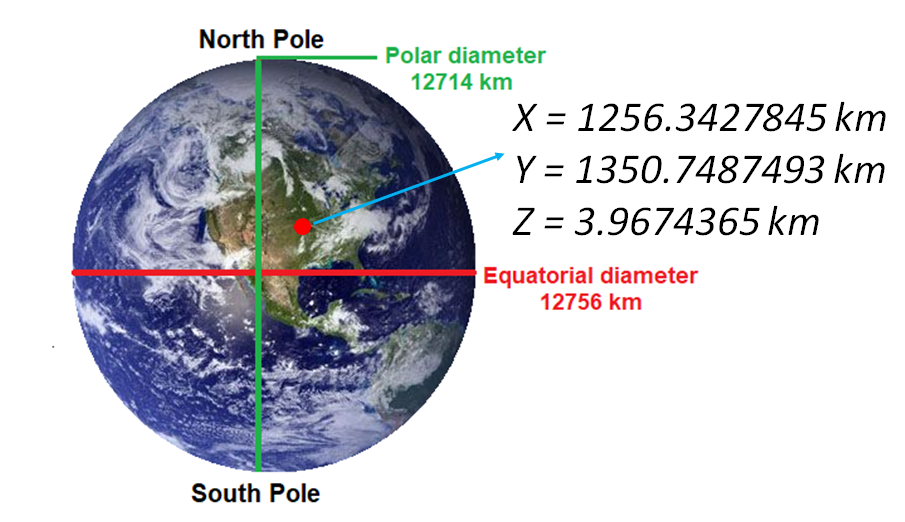
In global navigation satellite system (GNSS), estimated positions on earth, especially with Earth centre earth fixed (ECEF) coordinate system, can have values that are in thousands of km with the precisions that are up to 0.1 mm.
Because, the ECEF coordinate system follows the size of the earth radius, hence it values can be up to 6378 km. With a high-end global positioning system (GPS) receiver, the resolution can be up to 0.1 mm.
Hence, we can have a very large number of $6378 km$ with very small precision of $0.1 mm$. If we present the number in $km$ unit, we will get $6.3780000001\times 10^{9}$ that has 11 digits.
The data type assigned to a variable should have, then, at least 50 binary bits that can represent up to 15.05 decimal digits (calculated form the above formula).
In C/C++ or other programming language, we can use 64 bits data type double to represent the variables.
From this case, determining the correct data type for a variable is essential for GNSS (such as GPS) signal processing.
As a quick comparison, in manufacturing, it is common that the precision of a unit is up to 3 to 4 magnitude lower than the unit. For example, products or geometries with unit of measurement is in $mm$ (few mm, eg. 200.005 mm), their precision requirement is in $\mu m$ or in $0.1 \mu m$ or $sub-\mu m$.
Another case in manufacturing is that, when a measured value in hundreds of micrometre, very often the precision is in nanometre. Hence, for the case in manufacturing, we may need 6 or 7 decimal digits. The number of required bits to represent this decimal digits requirement can be 28 bits.
The question is, when in future the accuracy of GNSS is significantly improved, to let say 0.001 mm or even better, it can be problematic to represent the value with current common data types in programming language.
Conclusion
In this post, the importance of assigning a correct data type for variables in programming languages is presented.
Data type represents how many binary bits representation a variable can have to represent numbers.
A correct data type is when we assign a variable with correct number of bits that can represent decimal digits more than the decimal digit of numbers the variable will contain.
An incorrect data type assignments will cause a logic errors at run time that are difficult to debug. Hence, the programming productivity and the software quality will significantly decrease.
We sell all the source files, EXE file, include and LIB files as well as documentation of ellipse fitting by using C/C++, Qt framework, Eigen and OpenCV libraries in this link
You may find some interesting items by shopping here.