CMM measurement uncertainty estimation: ISO 15530-4
The mathematical model of CMM measurements is very complex to reconstruct. ISO 15530-4 presents a method to estimate CMM measurement uncertainty without the need of the mathematical model of CMM measurements.
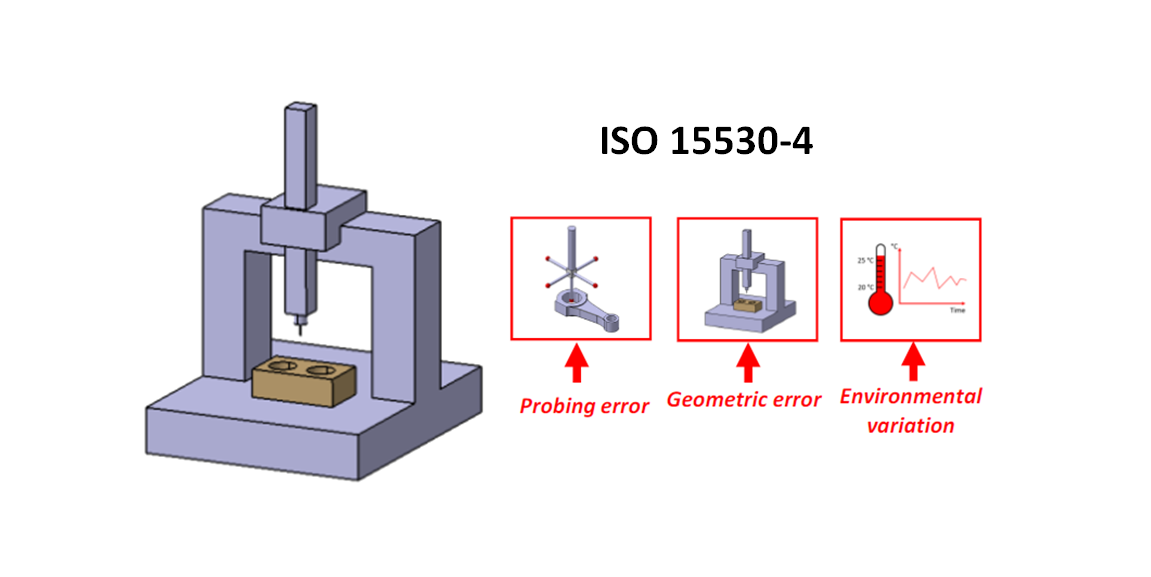
The mathematical model of CMM measurements is very complex to reconstruct. ISO 15530-4 presents a method to estimate CMM measurement uncertainty without the need of the mathematical model of CMM measurements.
In this post, the method of ISO 15530-4 will be presented and discussed. This method is very appealing, compared to ISO/DTS 15530-2 and ISO 15530-3. Because, beside the method does not require mathematical models of CMM measurements, the method is very flexible, cheap and fast to implement.
This ISO 15530-4 is very promising to be used to estimate “task-specific uncertainty” for CMM measurements.
The evaluation and validation methods of ISO 155340-4 are also presented and discussed.
Let us go into the details!
(Note: All 3D illustrations were created by using a CATIA 3D modelling software)
READ MORE: CMM measurement uncertainty estimation: Relevant uncertainty contributors

CMM uncertainty: ISO 15530-4
The method of ISO 15530-4 is a method to estimate coordinate measuring machine (CMM) measurement uncertainty by using Monte-Carlo (MC) simulation.
ISO 15530-4 method, used to estimate CMM measurement uncertainties that are “Task specific” uncertainty, is motivated from several drawbacks found in the previous ISO/DTS 15530-2 and ISO 15530-3.
The main drawback of ISO/DTS 15530-2 is that this method requires a relatively long time to perform the procedure to estimate CMM measurement uncertainties. Hence, this method is not very suitable for production lines that have short “tact time”.
In addition, ISO/DTS 15530-2 method requires measurements with different orientations. Hence, if a part has large size, it is very difficult to position the part at different orientations.
The main drawback of ISO 15530-3 is that this method requires a calibrated artefact with very similar shape with the part to measure. If, the part to measure has a complex shape, then it is very difficult and also very expensive to provide a calibrated version of the part.
This expensive cost and time consuming for preparing the calibrated artefact can only be justified if the part is produced in high-volume.
The main advantage of ISO 15530-4 method
- Flexible
This ISO 15530-4 method can be implemented for various types of measurement with different conditions without making new calibrated artefact and repeating measurements.
- Cheap
This means that ISO 15530-4 is relatively cheaper compared to the other ISO/DTS 15530-2 and ISO 15530-3. Because there are no repeating measurements at different orientation and no calibrate artefact.
- Easy to implement
The method is easy to implement because there is no need for expert operator as long as the simulation has been programmed.
- Minimal operator involvement
This method is by using computer calculations that are repeated in a large number. This process can be performed automatically without an operator supervision.
- Fast
This method is fast because there is no need of making many measurements with different positions and orientations (ISO/DTS 15530-2) and without the need to wait a calibration artefact to be manufactured and calibrated (ISO 15530-3).
The main steps of ISO 15530-4 method are shown in figure 1. In figure 1, the ISO 15530-4 has two main parts: steps shown in blue colour and steps shown in red colour.
The “blue” colour step is a real CMM measurement of a part. This measurement is only done once just to take real points from the part surface. These points are then will be used for MC simulation. These real captured points replace the mathematical model of the measurement.
The “red” colour step is the MC simulation procedure. The simulation used the previously real captured points as the replacement of the mathematical model of the measurement. In the MC simulation, these points are then perturbed by adding noise to the point coordinates. The noise considers relevant uncertainty sources of the CMM measurements.
The noise from the uncertainty sources follow certain probabilistic distributions. This point perturbation process is repeated in a large number of simulations run.
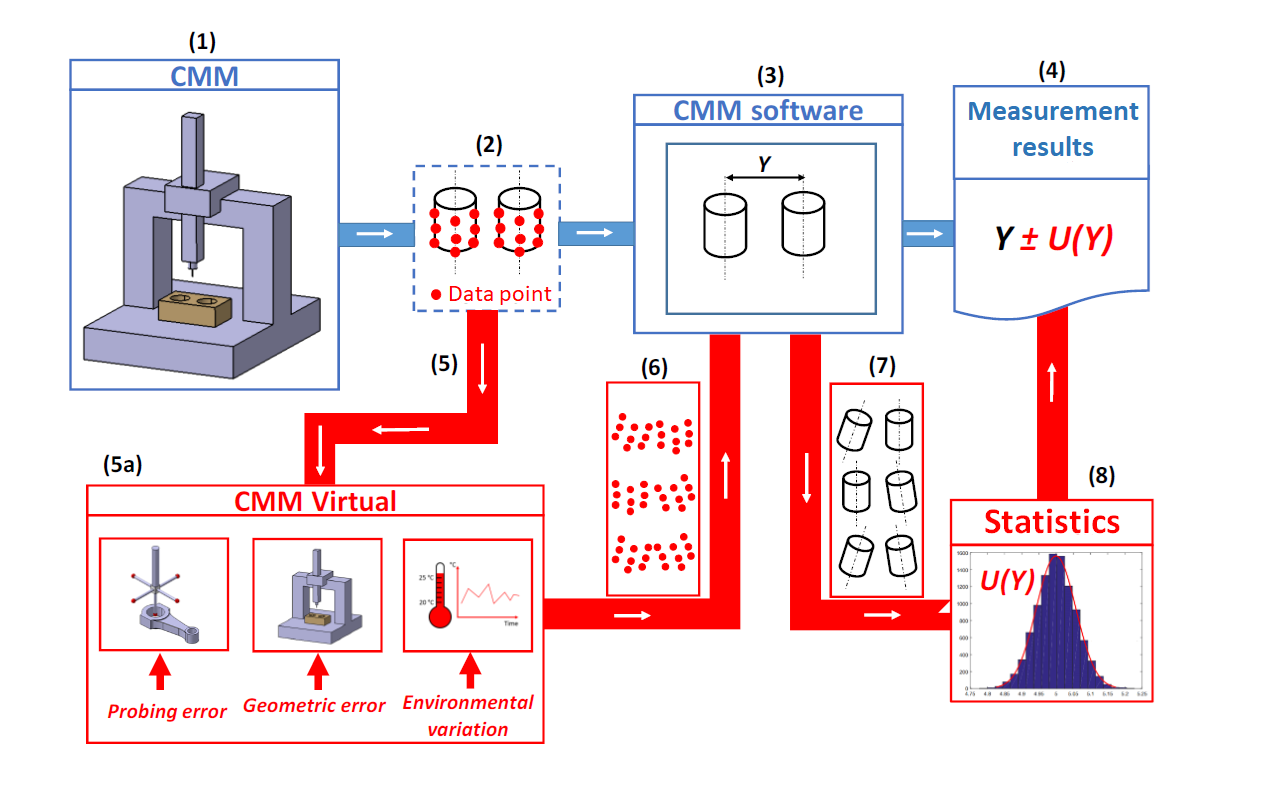
Detailed explanation of ISO 15530-4 procedures
The detailed procedure for ISO 15530-4 is as follow (following figure 1 above):
Part 1 (Blue line): Measurement estimation
This part is the first step to implement ISO 15530-4 method. The main idea of this part 1 is to replace the mathematical model of a CMM measurement.
The detailed steps of part 1 are:
- 1. A real measurement of a part is carried out by using a CMM to obtain measurement points. The CMM can be tactile (contact) or optical (non-contact). The measurement points are the replacement of the CMM measurement mathematical model.
- 2. The obtained measurement points are in the form of 3D point cloud obtained by the CMM.
- 3. The 3D points (point cloud) are the processed with a certain measurement algorithm, for example, least-square fitting (for size or dimensional measurement, for example diameter and length) or minimum-zone fitting (for geometrical measurement, for example flatness, roundness and perpendicularity)
- 4. From the measurement processing with one of the algorithms, a measurement $Y$ is obtained. In this part, only the measurement results $Y$ is obtained. But, the measurement uncertainty is not yet estimated. To estimate the measurement uncertainty, then part 2 of ISO15530-4 should be performed by using MC simulation.
Part 2 (Red line): Uncertainty estimation
This part is to estimate the measurement uncertainty of $Y$ (previously obtained from part 1) by using MC simulation. This part 2 is repeated in a large number of iterations to collect results in each iteration and then to perform statistical analysis from the collected or stored results.
The steps from (5) to (8) are performed iteratively as follow:
- 5. In this step, the collected 3D points (from part 1) are used as inputs for MC simulation. These data points represent the mathematical model of a CMM measurements.
- 5a. This step is the core or fundamental of the MC simulation according to ISO 15530-4. In this step, the obtained 3D points are given perturbations (adding noise to the points). These perturbations represent various types of relevant uncertainty contributors for CMM measurements, such as CMM geometrical error, probing error and error due to environmental effects.
The perturbation process is a mathematical process that is by applying geometrical transformation on the original (obtained) 3D point.
- 6. In this step, various types of new 3D data points (after being perturbed). These newly perturbed data points are then processed by using the same algorithm used to calculate the measurement results $Y$ (in part 1).
- 7. Each measurement result $Y_{sim}$ from each iteration is stored.
- 8. From all stored $Y_{sim}$, the standard deviation $\sigma$ of $Y_{sim}$ is calculated to estimate the measurement uncertainty $u(Y)$. After that, we add (sum-squared-root) this estimated uncertainty $u(Y)$ with other uncertainty contributors that are not considered in the simulation. The total estimated uncertainty is then $u_{c}(Y)$. Hence the complete measurement result can be presented as $Y \pm 2 \times u_{c}(Y)$.
READ MORE: CMM measurement uncertainty estimation: ISO 15530-3
- TUTORIAL 3D tolerance stack-up analysis – A package containing PDF files, MATLAB scripts and CAD files that show in detail how to perform 3D tolerance analysis with a real case study.
Evaluation and validation of ISO 15530-4 method
After the MC simulation has been performed and the measurement uncertainty has been estimated, we need to carry out evaluation and validation of the estimated uncertainty.
ISO 15530-4 evaluation
The final results of uncertainty estimations by using ISO 15530-4 method should be combined with other uncertainty contributors that are relevant to CMM measurements but are not considered or included in the MC simulation.
To combine uncertainty values that are estimated by the MC simulation with other uncertainty contributors, it can be calculated as follow:
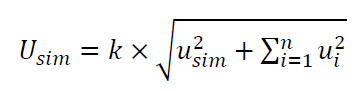
Where $u_{sim}$ is the standard uncertainty obtained from an MC simulation. $u_{i}$ is the standard uncertainty from the $i-th$ contributor that is not considered in the MC simulation ${i=1,2,3,…,n}$.
If all the relevant uncertainty contributors are considered or included in the MC simulation, then the total estimated CMM measurement uncertainty is the final uncertainty that produced by the MC simulation.
ISO 15530-4 validation
There are several methods to validate whether an uncertainty estimated by using the MC simulation is valid and can represent the real condition of a measurement.
In ISO 15530-4, those validation methods are:
· Validation by comparing with real CMM measurements
· Validation by comparing with a reference uncertainty value (for example, a calibration certificate or a GUM calculation)
· Validation by investigating and analysing the results statistically form many measurements
The “validation by comparing with real CMM measurements” is explained in detailed as follow. This validation is quantified by calculating a plausibility value $E$. the plausibility $E$ is calculated as:
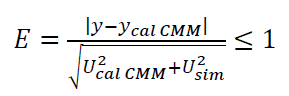
Where $y$ is a CMM measurement (either contact or non-contact CMM), $y_{calCMM}$ is a calibration value obtained by a higher-accuracy CMM, $U_{calCMM}$ is the expanded uncertainty of the calibration value $y_{calCMM}$, $U_{sim}$ is the expanded uncertainty from MC simulation combined with other uncertainty factors (ISO 15530-4).
The recommended number of measurements $y$ is at least 100 measurement repetitions. From each measurement repetition, $E$ is calculated. The result of the estimated uncertainty $U_{sim}$ is considered to represent real conditions if the value of $E \leq 1$ is $\geq 95 \%$ from the total calculated $E$.
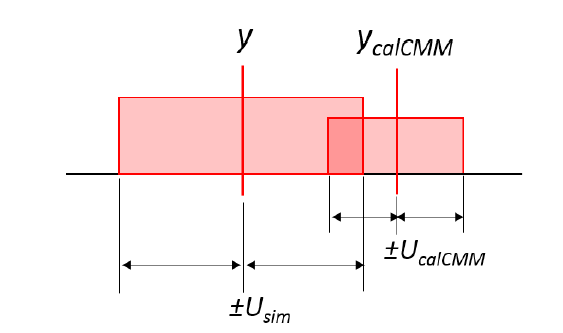
Figure 2 above shows the plausibility illustration. From figure 2, the estimated (expanded) uncertainty $U_{sim}$ is considered valid if there is intersection between $y$ associated with $U_{sim}$ and the interval $y_{calCMM}$ associated with $U_{calCMM}$.
READ MORE: CMM measurement uncertainty estimation: ISO/DTS 15530-2
Conclusion
In this post, the Monte-Carlo simulation method to estimate CMM measurement uncertainty based on ISO 15530-4 has been presented and discussed.
The main benefit of ISO 15530-4 is that the estimation method does not require the mathematical model of CMM measurements.
Instead, the method only requires a real CMM measurement to capture points on a part surface. These captured points are the substitute for the mathematical model of the measurement.
This uncertainty method is flexible, fast and cheap to perform. Hence, this ISO 15530-4 is an important CMM measurement uncertainty estimation method to be understood.
You may find some interesting items by shopping here.
