CMM measurement uncertainty estimation: ISO/DTS 15530-2
ISO/DTS 15530-2 provide a way to estimate coordinate measuring machine (CMM) measurement uncertainties without using any complex calibrated artefacts. Instead, only a performance verified CMM and a standard calibrated gauge block are needed.
ISO/DTS 15530-2 provide a way to estimate coordinate measuring machine (CMM) measurement uncertainties without using any complex calibrated artefacts. Instead, only a performance verified CMM and a standard calibrated gauge block are needed.
This is a bit controversy since there is no reference artefact, representing or similar with a measured part, that creates the traceability link to the definition of metre.
However, the requirement of a CMM that is used should be periodically performance verified and required a common calibrated gauge block length measurement becomes the argument to create the traceability chain.
Because, during the CMM performance verification, a calibrated or reference gauge block or length standard is required and is considered as the way to establish the CMM’s traceability.
Let us go into details about the ISO/DTS 15530-2!
(Note: All 3D illustrations were created by using a CATIA 3D modelling software)
READ MORE: CMM measurement uncertainty estimation: Relevant uncertainty contributors

CMM uncertainty: ISO/DTS 15530-2
ISO/DTS 15530-2 is a method to estimate the uncertainty of dimensional and geometrical measurements using CMM.
The main procedure to estimate CMM measurement uncertainties by using ISO/DTS 15530-2 is to repetitively measure a workpiece at different positions and orientations.
The name of this ISO/DTS 15530-2 method is multi-measurement strategy.
This method does not use any complex calibrated or reference artefacts except a common standard gauge block. That is, this method is flexible for various type of complex CMM measurements.
In addition, since there are no calibrated artifact requirements except a commonly used gauge block, the calibration cost will be relatively low.
The main requirement to implement this ISO/DTS 15530-2 method is by using a CMM that has been periodically performance verified and that the CMM works in its manufacturer specification.
The traceability chain is argued to be established from the periodically performance verified CMM and from a gauge block measurement correction. The performance verification of the CMM has been conducted by measuring calibrated or reference gauge blocks at different length covering at least 66% of the measuring volume of the CMM.
A slight additional modification of this method by measuring a few gauge-block can be added to solidify the traceability of the CMM measurement of which measurement uncertainties are quantified.
Procedure of ISO/DTS 15530-2 to estimate CMM measurement uncertainties
The procedure to estimate CMM measurement uncertainties based on ISO/DTS 15530-2 is as follow:
- The total number of measurements required are 20 measurements
The total of 20 measurements consists of five repetitions for each four different workpiece orientations and positions.
Figure 1 below shows four different orientations (and positions) for, in this case, a piston diameter measurement. The main goal is to estimate the piston diameter as well as the uncertainty of the diameter measurement.
In figure 1, the piston orientations are intentionally varied as well as the location of where the piston is placed inside the CMM measuring volume.
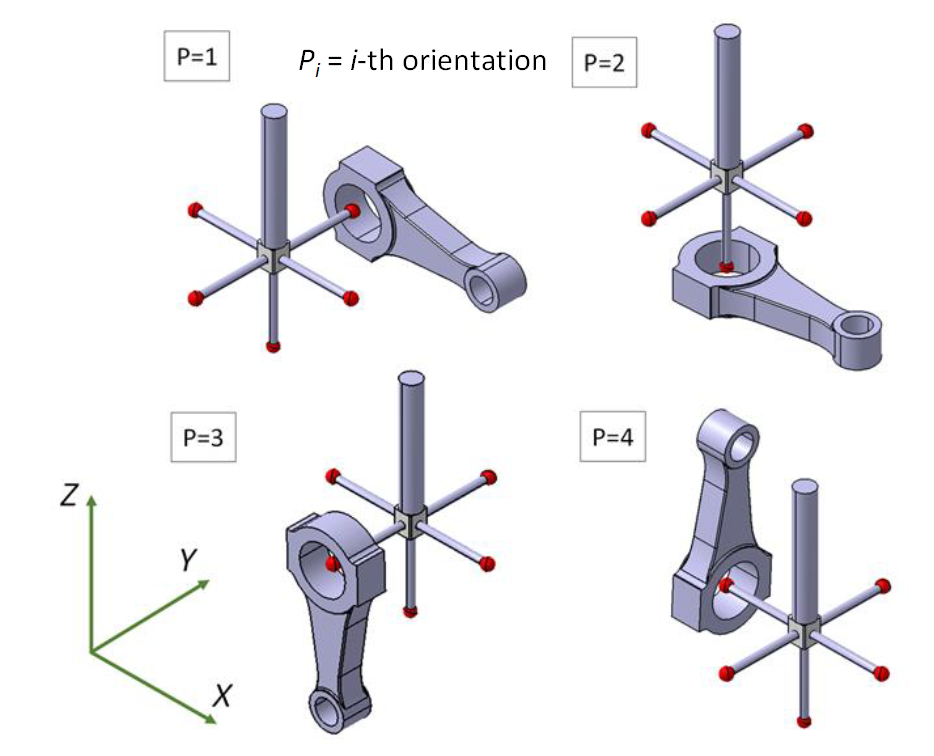
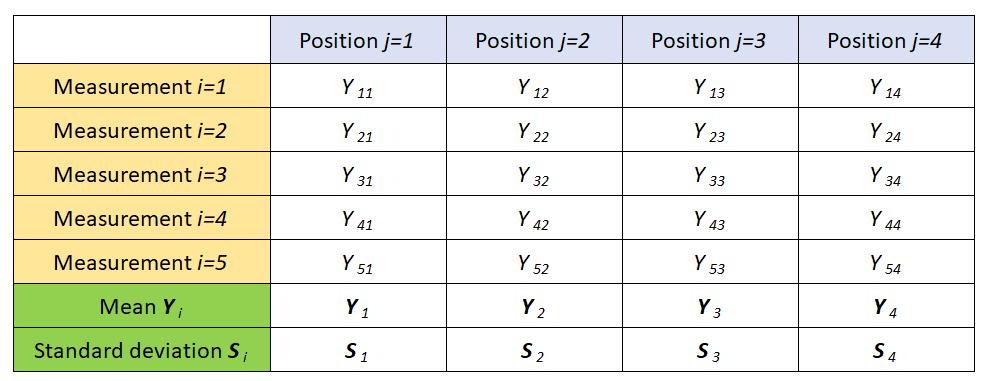
Figure 2 below shows the measurement data management when performing the procedure of ISO/DTS 15530-2.
In figure 2, a total of 20 measurement data will be collected. The statistics of these collected data will be exploited to estimate the uncertainty of a workpiece measurement with CMMs.
- The stylus tip used for the uncertainty estimations should be qualified (see CMM probe qualification process) instead of using the previous stylus qualification data
The reason of using a freshly qualified stylus tip data is to minimise the uncertainty originated from probing error and stylus tip geometry imperfection. Because, in reality, the shape of a stylus tip will be deformed over time in addition to geometrical defect of the tip due to manufacturing error.
- The recommendation is to use various type of sampling point locations for each position and orientation
The reason of using different point locations is so that the uncertainty estimated by this method also covers uncertainty due to sampling strategy and the imperfection of a measured surface.
From figure 1 above, the four different positions and locations of the workpiece is to consider the geometrical error of the CMM in the uncertainty estimation and the estimated uncertainty is comprehensive and valid.
The geometrical errors are for example squareness error, angular error and scale error. These geometrical errors of the CMM will be represented by the imperfection of the CMM’s axes motions.
A recommendation to implement ISO/DTS 15530-2 is to use a “star-shape” stylus configuration to be able to access a part’s feature to measure at different orientations (see figure 1 above).
From figure 2 above, measurements are divided into four parts based on the orientation (location) of a measured part, that is $j-th$ orientation $\{j=1,2,3,4\}$. And, on each part orientation, five measurement repetitions are performed $\{i=1,2,3,4,5\}$.
Different measurement samplings (locations of sampled points) are recommended to also consider the uncertainty of CMM sampling strategy.
From each part orientation group (figure 2 above), statistical mean and standard deviation from the five measurement repetitions are calculated.
The calculations derived form data in the table shown in figure 2 are as follow:
1. $u_{rep}$:
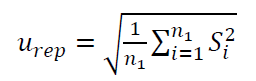
Where $n_{1}$ is the number measurement repetitions on each orientation (location).
The calculation of $Y_{i}$ and $S_{i}$ are:
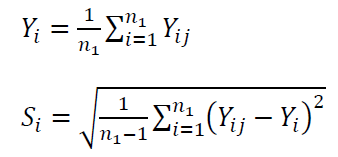
2. $u_{geo}$:
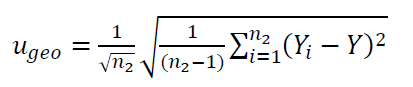
Where $n_{2}$ is the number of different orientations (locations).
$Y$ is calculated as:
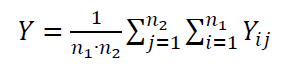
3. $u_{corr}$:
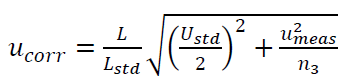
Where $L_{std}$ is the length of calibrated gauge block, $L_{i}$ is the length of the $i-th$ measured gauge block and $U_{std}$ is the expanded uncertainty (k=2) obtained from the calibration certificate of the gauge block.
The value of $u_{meas}$ and $L$ are formulated as:
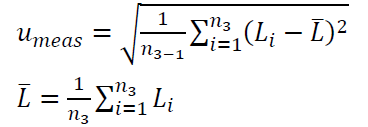
4. Length correction calculation
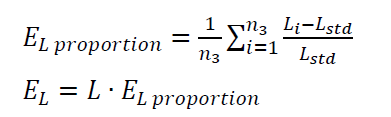
Where $n_{3}$ is the number of gauge block length measurements. Commonly, $n_{3}=3$ and $L$ is the measured length on a workpiece.
The explanation of each uncertainty contributors mentioned above are as follow:
- $u_{rep}$: uncertainty contributors from CMM repeatability, form error of a part, surface quality of a part, sampling strategy and dirt on a measured surface
- $u_{geo}$: uncertainty contributors from CMM geometry error, stylus error, tip error, fixturing error and alignment error
- $u_{corr}$: uncertainty contributors from errors caused by a reference gauge block measurement error. This correction is only applicable for length and size measurement but not for form measurements.
- $u_{temp}$: uncertainty contributors from temperature variation of the room where a CMM measurement is performed and from error on the coefficient thermal expansion of a measured part
- For length and size measurement, the measured length and size L is:
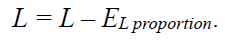
Finally, the uncertainty estimation based on ISO/DTS 15530-2 is calculated as:
- Uncertainty estimation for length and size measurements (dimensional measurements) such as diameter and depth measurement:
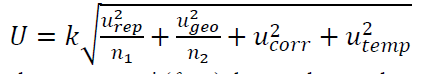
- Uncertainty estimation for geometrical (form) and angle measurements, such as flatness and perpendicularity:
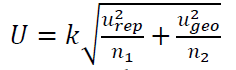
READ MORE: The fundamental concept of metrology

The benefit and disadvantages of ISO/DTS 15530-2 method
The benefits of using ISO/DTS 1553-2 for CMM measurement uncertainty estimation are:
- This method can be applied efficiently for low volume production and high variety of parts
- This method reduces the uncertainty contributor from the volumetric (geometrical) error of a CMM by using the averaging effects from repetitive measurements at different positions and orientations
- This method is very suitable to calibrate a workpiece measured by a CMM
The disadvantages of using ISO/DTS 1553-2 for CMM measurement uncertainty estimation are:
- The procedure of this method requires a relatively longer time than the procedure based on ISO 15530-3
- This method is not efficient to be implemented for part measurement in high volume production
Conclusion
In this post, the method to estimate CMM measurement uncertainty based on ISO/DTS 15530-2 has been explained and discussed.
This method is very suitable for low volume part production and for a single or few part calibrations.
The main concept of this uncertainty estimation method is that this method does not require any complex calibrated or reference artefact. Instead, this method only follows procedures to measure a workpiece at different positions and orientations repetitively.
However, this method requires a CMM to be periodically performance verified since the traceability chain is argued to be established from the performance verified CMM.
This method is considered to have a low calibration cost. Because complicated calibrated artefacts are not needed except for only a commonly used gauge block.
You may find some interesting items by shopping here.
