Sampling strategy for coordinate measuring machine (CMM) measurements
In any CMM measurements, especially with a tactile-CMM, sampling strategy is very important. This Sampling strategy in CMM measurement affects not only measurement performance, but also measurement accuracy!
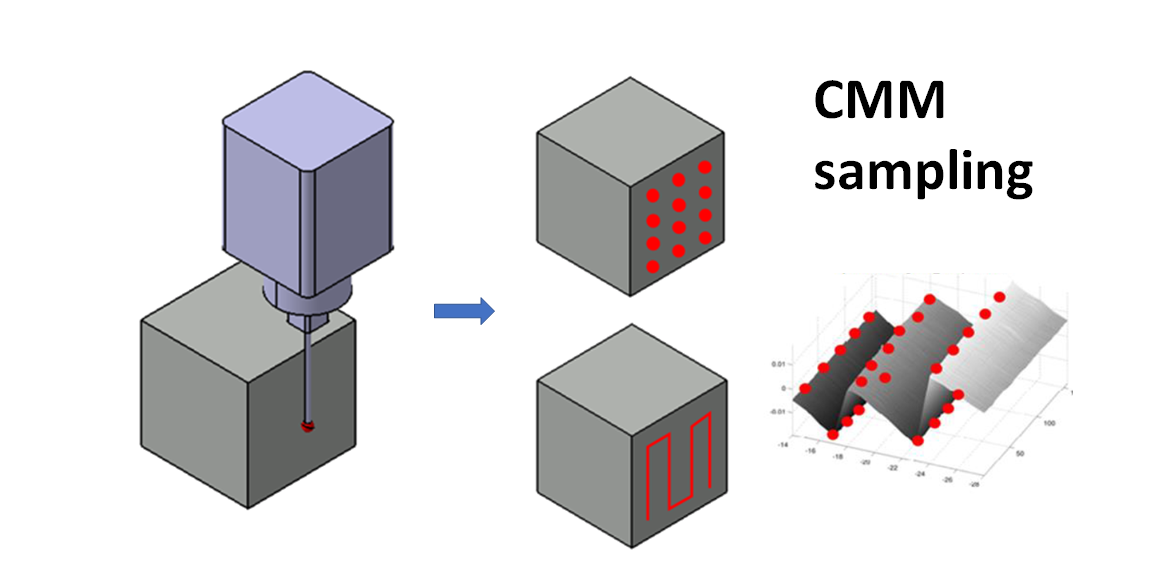
In any CMM measurements, especially with a tactile-CMM, sampling strategy is very important. This Sampling strategy in CMM measurement affects not only measurement performance, but also measurement accuracy!
Sampling strategy is defined as a strategy (the number of points and the location of the points) to probe or capture points on a surface measured by using a CMM.
A good sampling strategy is a strategy that is able to find the best trade-off or compromise between measurement time and measurement accuracy.
Too many sampled points in a CMM measurement will increase the measurement time and require more computational power of the CMM machine and computer (due to many points to process). Hence, this situation will reduce the CMM performance.
Otherwise, too few sampled points in a CMM measurement will reduce measuring time. However, if the sampled points is not enough, the mathematical fitting process, applied to the sample points, to a relevant geometry or the reconstruction of the geometry to derive a measurement will be ill-defined and then will increase measurement error!
In general, sampling strategy is classified into three types:
- Blind sampling strategy
- Process fingerprinting (manufacturing signature) base sampling strategy
- Adaptive sampling strategy
Let us discuss in more details!
READ MORE: General procedures to operate a tactile coordinate measuring machine (tactile-CMM)

Blind sampling strategy
Blind sampling strategy is the most common and used strategy to probe or capture points on a measured surface. Within the class of blind sampling strategy, uniform sampling is the most used strategy.
The blind sampling strategy is commonly used because most of the time information that we have about a measurement is only the nominal geometry and dimension, and tolerance of the feature or geometry on a part that we want to measure.
The pattern of blind sampling strategy has been defined before a CMM measurement is conducted and is fixed during the CMM measurement process.
In general, blind sampling is performed by probing points on the surface of a measured part by using uniform or random methods, especially where to sample or probe points. In addition, the probed points are spread across the entire surface of the measured part.
Figure 1 below shows examples of blind sampling strategies using uniform sampling. In figure 1 below, several geometries to measure and the pattern of sampling points for line, circle, plane and cylinder geometries are presented.
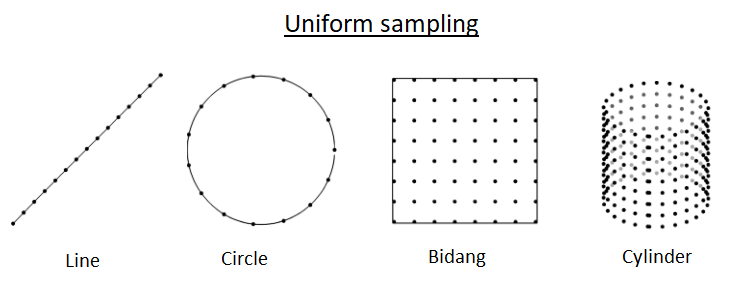
For blind sampling strategy with uniform pattern, the sampling should always follow Nyquist sampling theorem to determine the number of sampled points and distance between the points.
The reason is that, by following the Nyquist theorem for sampling, we can sufficiently obtain points to faithfully reconstruct the shape of a measured surface and subsequently, we can perform dimensional and geometrical measurements. The shape reconstruction is performed by applying a geometrical fitting process.
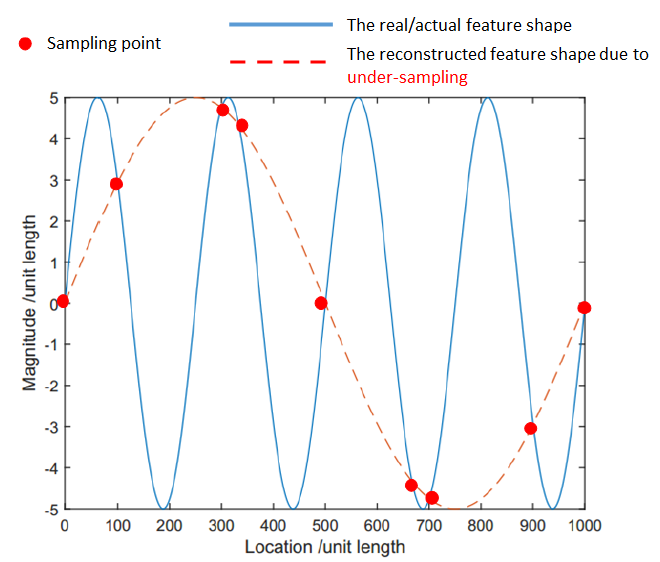
The Nyquist sampling theorem (for unlimited bandwidth) states that, considering geometrical reconstruction applications, if a geometry (for example a sinusoidal curve) is sampled with uniform sampling by using a sampling frequency (the number of sampled points/sample size) that is more than two times of the frequency of the sampled geometry (for example the sinusoidal curve), then the geometry (in this example, the sinusoid curve) can be faithfully or correctly reconstructed.
Otherwise, if the sampling frequency is less than two times of the frequency of the geometry or curve, then the geometry or curve cannot be faithfully reconstructed. This incorrect reconstruction will cause a significant measurement error.
Figure 2 below describes the concept of Nyquist sampling theorem. In figure 2 below, a sinusoidal geometry (in this case a curve) that is sampled with sampling frequency to be less than two times of the frequency of the sinusoid curve. In this situation, the original sinusoid curve cannot be correctly reconstructed.
Uniform sampling strategy, if performed with a correct sampling frequency (sample size), is an effective method to capture points on a surface. Because, this method guarantee that all captured or probed points represent all feature shapes (geometry) on a measured surface.
However, in general, a uniform sampling will require a large amount of sampling points and cause a long measuring time. This long measuring time causes an increase on inspection cost and reduction on productivity.
Hence, to overcome the drawback of uniform sampling strategy (that is relatively long measuring time), several semi-random sampling methods are proposed.
These semi-random sampling strategies try to reduce the number of points to probe or capture while maintaining that all the probed points cover and represent all relevant features on a measured surface.
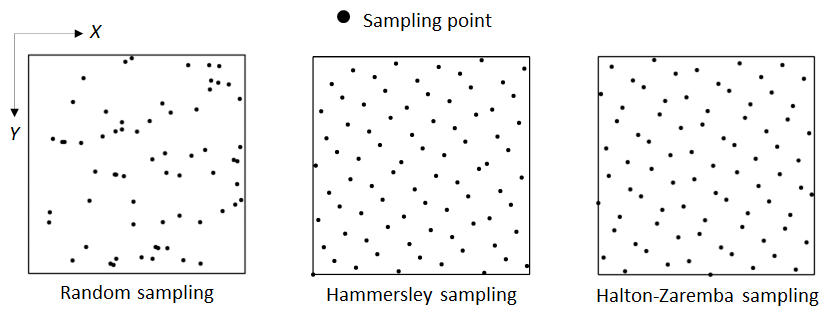
There are two famous semi-random sampling strategies, that are Hammersley and Halton-Zaremba sampling methods.
The Hammersley sampling strategy determines the location to probe or detect points on a surface by this formula:
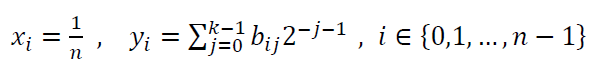
Where $x_{i}$ and $y_{i}$ are the coordinate or location of point $i$ to probe (note that the location is normalised to be between 0 and 1 value, representing minimum and maximum coordinates. We need to re-scale the value to get the actual location of $x$ and $y$). $n$ is the number of sampling point (sample size). $b_{i}$ is a binary representation of $i$ and $b_{ij}$ is the $j-$th bit of $b_{i}$ with value either 0 or 1. $k=[log_{2} n]$.
The Halton-Zaremba sampling strategy determine the location to probe or detect points on a surface by this formula:
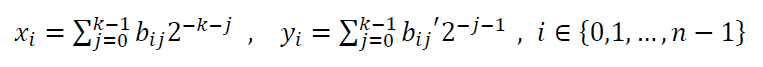
Where $b_{ij} ‘ = 1-b_{ij}$ if $j$ is odd, or $b_{ij} ‘ = b_{ij}$ if $j$ is even.
Figure 3 below shows comparisons among random, Hammersley and Halton-Zaremba sampling strategies.
Halton-Zaremba sampling strategies is claimed to give a better flatness measurement than using random and Hammersley sampling strategies [1].
- Grammar Rules: Everything you need to know but never learnt in school – A book about how to make efficient and concise sentences to writing with military precision!
Process fingerprinting (manufacturing signature) based sampling strategy
Process fingerprinting (manufacturing signature) based sampling strategy is defined as a sampling strategy that uses some a-priori knowledge of the fingerprint or signature of a manufacturing process to optimise a measurement process (reducing measuring time while improving measurement accuracy).
Process fingerprinting (manufacturing signature) is a “unique” trace on a part manufactured or processed by a specific method or machine with specific process parameters.
For example, a side milling process will have a trace on a part in the form of sawtooth-surface shape [2].
This sampling strategy, thanks to a-priori information from the fingerprint/signature of a process, has a minimised sampling points with pre-determined locations. Like the blind sampling strategy, the number of points in this sampling strategy is fixed during a measuring process.
The determination of the number of sampling points and sampling locations is carried out by using the information on a surface due to a process fingerprinting. Hence, the sampling point determination is such that the sampled points cover the area on a measured surface with maximum geometry deviation (with minimal number of points).
The implementation of process fingerprinting sampling strategy is not difficult and can be applied by using a general CMM machines.
The main drawback of this sampling strategy is that this sampling strategy is specific (only can be used) for a specific process with specific process parameters. Because, if the same process has undergone a process parameter change, the process will have different fingerprinting and subsequently different process fingerprinting sampling strategies.
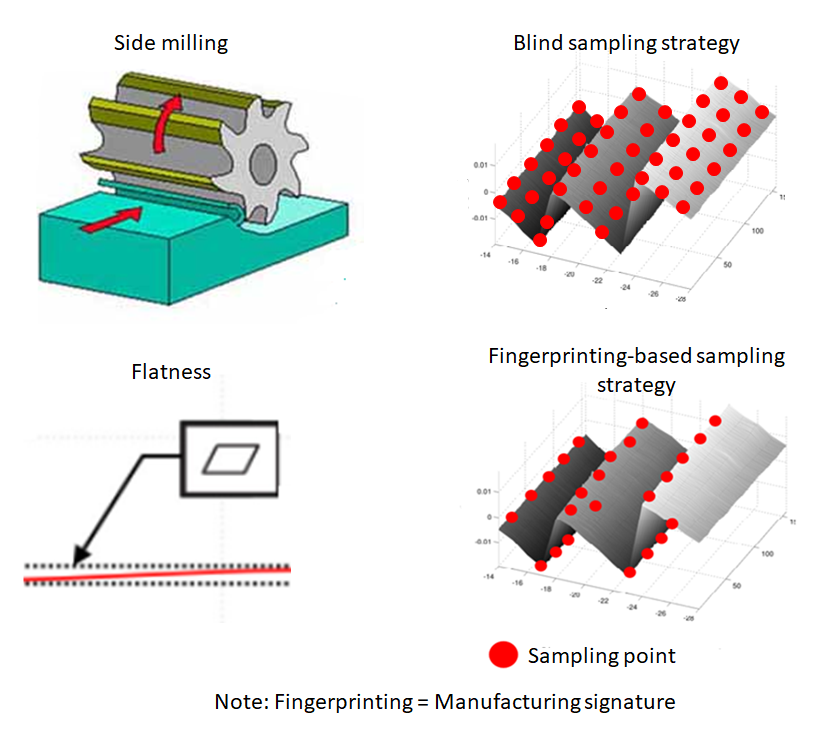
Figure 4 below shows an example of process fingerprinting sampling strategy for flatness measurement of a side milled surface. In figure 4, a side milling process of a metal surface is shown.
The metal surface has a flatness tolerance that should be verified by using a tactile-CMM.
In figure 4, if a blind sampling strategy is performed, then the sampling points are spread throughout the surface including area that does not give any significant information for flatness measurement (the area that does not have the maximum deviation, that is not the peak and valley of the surface).
In fact, for flatness measurement, the areas that are critical to determine a flatness value are the peak and valley of the surface. These areas should be covered by the sample points.
The side milling process has a saw-tooth fingerprinting on the surface (figure 4).
If a process fingerprinting sampling strategy is implemented, then the sampling points only focus on the peak and valley area of the surface. By doing this, the total number of sampled points can significantly be reduced and measuring time will be shortened.
READ MORE: The probing system of tactile-CMM: Vector diagram and qualification process
Adaptive sampling strategy
Adaptive sampling strategy is a sampling strategy where the number of sampling points and their locations on a measured surface is not fixed during a measurement. Instead, the number of points and locations can change or adapt based on the analysis and real condition of a part feature on an actual measurement process.
This sampling strategy starts by initially taking or probing several points on a surface. Then, a mathematical analysis is applied to the initially probed points to determine the next number of points and their location to sample or probe.
The main goal of this sampling strategy is to find a critical feature to measure during a measurement (since we do not have a-priori information of the process fingerprinting) and sampled points on the critical feature with minimal number of points to speed up measuring process and maintain high accuracy measurement.
Until now, this adaptive sampling strategy is an active research field, especially on tactile CMM. Because, to effectively realise an adaptive sampling strategy, an integration with automatic path-planning of a CMM measurement should be implemented.
Adaptive sampling strategy requires a specific procedure and analysis to determine the number of points and the location of the points to probe. Several criteria to determine the sampling points are:
- By fitting a spline on initially probed points to have a rough estimate of a surface shape and, based on this shape estimate, determine the next points to samples (their numbers and locations)
- By using a direct search method as in a numerical optimisation to find the minimum and maximum points on a surface equation. This surface equation is estimated from points that have been previously probed or captured.
- By using a kriging method based on spatial statistics. This kriging method can estimate a free-form surface from previously taken points to estimate the shape of a surface.
READ MORE: The probing system of tactile-CMM: The history, configuration and mechanism
Conclusion
In this post, the importance of a sampling strategy for CMM measurements has been discussed. The decision to select a sampling strategy will directly affect the measuring time and accuracy of a CMM measurement.
There are three main types of sampling strategy that have been discussed: blind, process fingerprinting (manufacturing signatured) based and adaptive sampling strategy.
The advantage of blind uniform sampling strategy is that it can be applied to general types of surface geometry and dimensional measurement. But, the measurement efficiency could be not high due to many sampled points required.
The advantage of process fingerprinting sampling strategy is that it can reduce sampling points while maintaining the same level of accuracy provided by uniform sampling. However, it can only be applied to a specific part produced with a specific process with specific process parameters.
The advantage of adaptive sampling is that it tries to combine the benefit from both blind and process fingerprinting strategy. That is, this adaptive strategy tries to minimise number of measurement points, but at the same time, it tries to cover important feature with higher geometrical deviation for CMM measurement. Despite these benefits, adaptive sampling still has challenges for the implementation.
References
[1] Kim, W.S. and Raman, S., 2000. On the selection of flatness measurement points in coordinate measuring machine inspection. International Journal of Machine Tools and Manufacture, 40(3), pp.427-443.
[2] Moroni, G. and Petro, S., 2013. Inspection strategies and multiple geometric tolerances. Procedia CIRP, 10, pp.54-60.
You may find some interesting items by shopping here.
We sell tutorials (containing PDF files, MATLAB scripts and CAD files) about 3D tolerance stack-up analysis based on statistical method (Monte-Carlo/MC Simulation).
