Vectorising linear sequence search in MATLAB programming
To significantly speed up the computation speed in MATLAB, the reduction of for loop should be minimised.
n MATLAB programming language, the execution speed of “for loop” is very slow compared to compiled languages such as C/C++. Hence, to significantly speed up the computation speed in MATLAB, the reduction of for loop should be minimised, meanwhile at the same time, the use of built-in function should be maximised.
The slow execution of “for loop” also applies to other interpreted languages other than MATLAB, such as Python.
In reality, complex programs, especially with advanced scientific algorithms, require “for loop” and “nested loop” to iterate through variables or computation, such as in a mathematical optimisation process.
It is impossible to avoid iterations in any complex programs.
In this post, we will present and discuss a method to speed up iteration by replacing “for (nested) loop” with a vectorising method.
An application example where this method can be implemented is for linear sequence search. We will show how this search iteration can be speeded up by avoiding using “for (nested) loop”.
Let us go to the discussion!
READ MORE: TUTORIAL: C/C++ programming with Qt framework, OpenCV and Eigen libraries for ellipse fitting from images
- Python Data Science Handbook: Essential Tools for Working with Data – A practical reference book in Python for breadth of computational and statistical methods that are central to data-intensive science, research, and discovery.
A well-known example of vectorisation: linearising a 2D matrix
As an introduction of vectorising method, we will revisit a well-known case. That is, vectorising a 2D matrix.
Vectorising a 2D matrix is a process to transform a matrix represented as 2D data structure into a vector represented by 1D data structure.
With 1D data structure, the iteration process to visit all the elements becomes faster compared to when the elements are in the 2D data structure.
Figure 1 below shows the illustration of vectorising a 2D matrix data structure into 1D vector structure.
In figure 1, the process is by vectorising the 2D structure in row-wise. That is, the second row will be beside the first row and the third row will be beside the second row and so on.
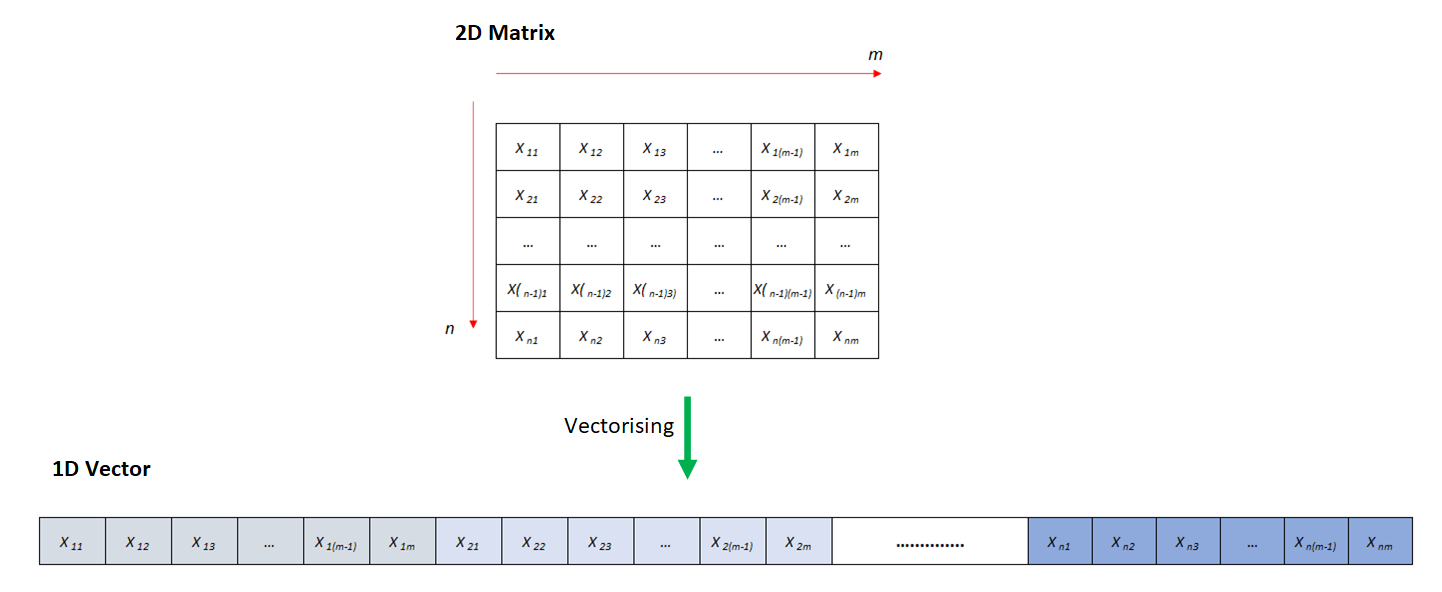
To access the element, instead of $data[i,j]$, the element access at $row i-th$ and $column j-th$ is $data[(i-1)*m+j]$ (since MATLAB index starts from 1. If the index start form 0, such as Python, then it becomes $data[i*m+j]$). Where $m$ is the column size.
Comparison of speed execution between a 2D matrix structure and 1D vector structure is as follow.
In the code section below, we use nested loop to iterate through all the element $i$ and $j$ of a $n \times m$ 2D matrix. The size of the matrix is $10000 \times 10000 $, that is it has $10^{8}$ elements. $n$ is the number of row and $m$ is the number of columns.
%2D matrix structure
tic
n=10000;
m=10000;
mat=rand(n,m);
for i=1:n
for j=1:m
element=mat(i,j);
end
end
t1=toc
The execution total time of using 2D data structure with nested loop $t1$ that is required to visit all the elements is $2.05s$.
Meanwhile, in the code section below, the 2D matrix is linearised into 1D vector by vectorisation process. the 2D matrix is now in 1D vector with size of $10000 \times 10000$.
To iterate all the elements of the vector, we only access 1D vector or array as follow.
tic
mat=rand(1,n*m);
m=1000;
for i=1:n
for j=1:m
element=mat((i-1)*m+j);
end
end
t2=toc
by implementing the vectorisation, the total execution time $t2$ to visit all the elements is $1.1s$. This total time is almost 50% faster compared to the t1 (the 2D matrix format).
From this example, we can see that a huge improvement in execution time can be obtained!
READ MORE: TUTORIAL: C/C++ implementation of circular buffer for FIR filter and GNU plotting on Linux
- Python for Data Analysis: Data Wrangling with Pandas, Numpy, and Ipython – A book that provides comprehensive guides for manipulating, processing, cleaning, and crunching datasets in Python.
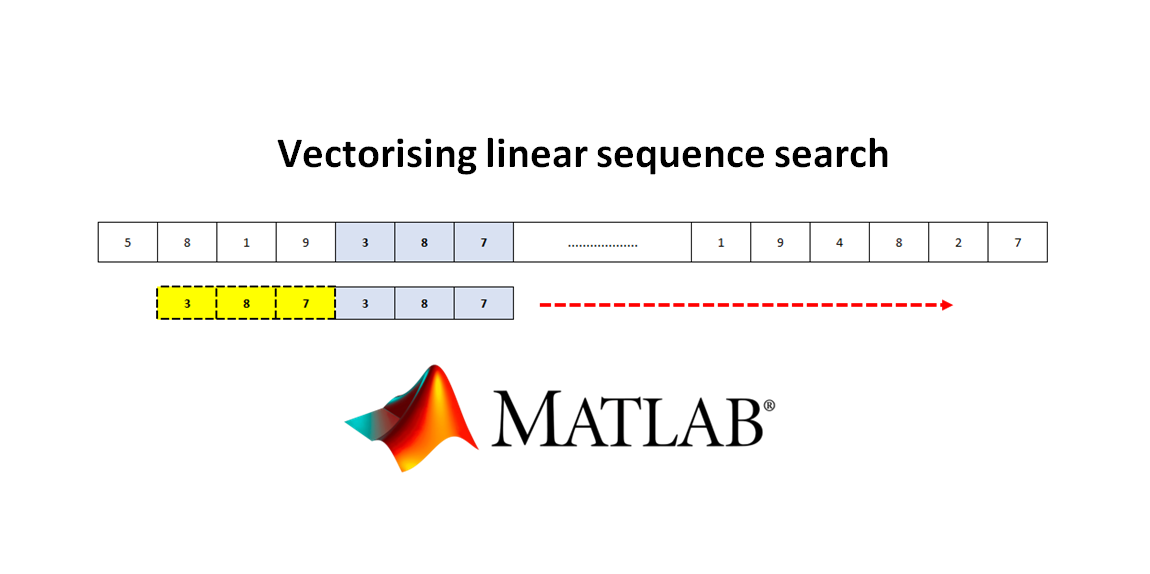
Vectorising linear sequence search
In this example a linear sequence search problem is presented. Linear sequence search is a process to find the location of a set of numbers in a long or much bigger size vector.
This problem is common to be found in many applications in programming. One of obvious applications is in radio frequency (RF) signal demodulation processes.
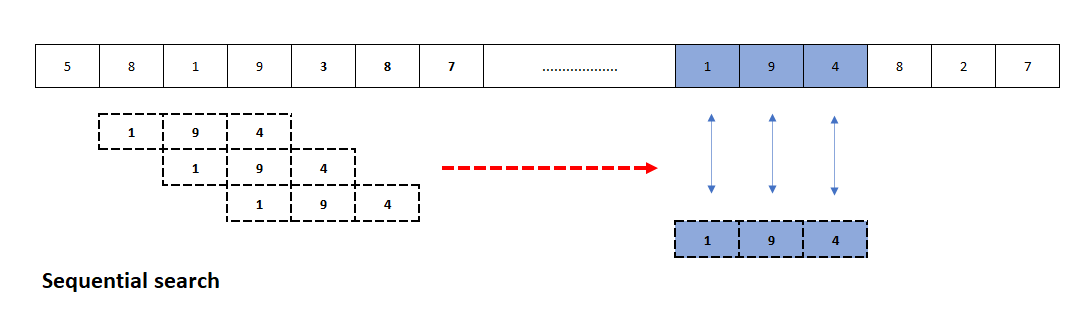
Figure 2 below illustrates the linear sequence search problem. In figure 2, a set of values $[1,9,4]$ needs to be found within a set of elements in a long vector. We need to find the index in the vector where the first value of the element to search is found.
The code below initialises the search element and the vector. We intentionally insert the set of the search element into the vector to exactly know where the location of the elements in the vector is.
length_data=length(search_element);
n=10000;
m=10000;
vec=rand(1,n*m);
%inserting the search-element into the matrix so we know exactly where they are
vec(10000:10000+length_data-1)=search_element;
The code section below shows the searching implementation by using nested loop (two loops, one loop is inside another loop). This nested loop is very inefficient in MATLAB execution.
tic
for ii=1:length(vec)-length(search_element)
counter_bit=0;
for jj=1:length(search_element)
if(vec(ii+jj-1)==search_element(jj))
counter_bit=counter_bit+1;
end
end
if(counter_bit==length(search_element))
start_index=ii
break;
end
end
t1=toc
By using the nested loop, the total execution time $t2$ to find the location of the search element in the vector is about $0.02s$.
The code section below implements vectorising method to eliminate the nested loop and to use a MATLAB built-in function (that is fast compared to loop command) implementation to search the element in the vector.
tic
for ii=1:length(vec)-length(search_element)
%idx_preamble=zeros(1,length(PREAMBLE));
counter_bit = sum (vec(ii:ii+length(search_element)-1) == search_element);
if(counter_bit==length(search_element))
start_index=ii
break;
end
end
t2=toc
From the vectorisation process and the use of MATLAB built-in function, the total execution time $t2$ to find the location of the search element within the long vector is about $0.01s$. That is, the search is around 50% faster than using the nested loop version before.
READ MORE: Beware of integer data type in computing

Conclusion
In this post, a vectorising method to reduce nested loop and utilise built-in function, and hence to speed up significantly the execution time, in MATLAB has been explained.
This method can also be applied to other interpreted languages, such as Python, that are slow in executing a loop command.
Two example applications for the vectorising method are given. One example is the most well-known example that vectorises a 2D matrix into 1D vector. The second example is vectorising a linear sequence search.
This linear sequence search process has many applications in programming, for example in radio frequency (RF) signal demodulation processes.
Hence, understanding vectorising method is very important!
You may find some interesting items by shopping here.
- Python for Data Analysis: Data Wrangling with Pandas, Numpy, and Ipython – A book that provides comprehensive guides for manipulating, processing, cleaning, and crunching datasets in Python.