Brief discussions on uncertainty contributors of GNSS-based positioning (Part 3)

Pseudorange is the distance between a global navigation satellite system (GNSS) satellite and a receiver when the offset of the receiver clock (with respect to GNSS timeline) is not yet corrected.

That is pseudorange is calculated as the multiplication between the travel time of a GNSS signal from the antenna phase centre of a satellite when the signal is transmitted (emission time) to the antenna phase centre of a receiver (reception time) and the speed of light [1,2,3].

Following the two previous posts on the principle of metrology and traceability, and the formation of navigation equations to calculate GNSS positioning, this post focuses on factors affecting the formation of pseudorange calculations.

Since the speed of light is commonly assumed to be constant, most factors affecting pseudorange calculation are those that affecting the travel time of GNSS signals from satellites to a receiver.

By the end of this post, readers will understand those affecting factors as well as can derive more details about uncertainty contributors that are relevant to pseudorange and then relevant to GNSS positioning.

READ MORE: Brief discussions on uncertainty contributors of GNSS-based positioning (Part 2)

Pseudorange formation

The basic equation of pseudorange is simple, that is:

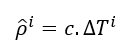
Where $c$ is the speed of light and $\delta T^{i}$ is the ranging signal from satellite $i$ to a receiver.

In general, $\delta T^{i}$ can be written as:

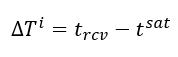
Where $t_{rcv}$ is the reception time of the signal at a receiver and $t^{sat}$ is the emission time of the signal from a GNSS satellite. Note that the time scale of the receiver (via the receiver clock) is different with the time scale of the GNSS satellite.

This distance is called “pseudorange” because this range is not representing the real geometric distance between a receiver and GNSS satellites. Because there are both systematic and non-systematic errors when calculating the travel time $\delta T^{i}$.

The systematic error is the receiver clock offset with respect to the GNSS timescale. Meanwhile, the random error can be from various factors due to radio propagation through atmosphere and other effects.

There are two main types of pseudorange formation:

• Code pseudorange measurement. This pseudorange is calculated from measuring the travel time of the PRN code (the ranging code) transmitted from a GNSS satellite to a receiver.
• Carrier phase pseudorange measurement. This pseudorange is calculated from measuring the travel time of the carrier phase transmitted from a GNSS satellite to a receiver.

Note that the “measurement” means by implementing signal processing and analysis to estimate the travel time of the PRN code or the carrier phase of GNSS signals.

To improve the accuracy and precision of pseudorange measurements, combination of code and carrier phase measurements at different frequencies can be used to cancel out some variation contributors.

There are two common types of GNSS positioning: standard point positioning (SPP) and precise point positioning (PPP):

• Standard point positioning (SPP) is a GNSS positioning based on code pseudorange measurement from single frequency GNSS signal, for example GPS L1 and GAL E1. This is the common GNSS positioning solutions based on mass market or low cost GNSS receivers.
• Precise point positioning (PPP) is a GNSS positioning based on at least both code pseudorange and carrier phase pseudorange and typically use a combination of multiple frequency of GNSS signals, for example GPS L1 and GPS L2 signals.

Two distinct properties between code pseudorange measurement and carrier phase (carrier) pseudorange measurement are [1,2,3]:

- Code pseudorange measurement is noisy. However, the measurement is continuous (unambiguous).

- Carrier phase measurement is precise. However, the measurement is discontinuous (ambiguous). This ambiguity can cause an unknown bias (systematic error) in the order of thousands of kilometres.

Code pseudorange measurement

Pseudorange obtained from code (PRN ranging code) measurements is the most common calculated pseudorange, especially for single frequency GNSS receiver.

Single frequency GNSS receiver is typically low cost as well as is found in mass market product.

The pseudorange of code measurement is formulated as:

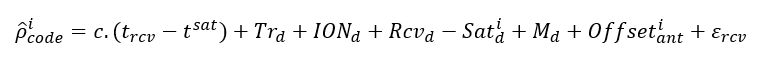
Where:

$t_{rcv}$ is the receiver clock offset from a GNSS timescale.

$t^{sat}$ is the satellite clock offset from a GNSS timescale typically caused by satellite atomic clock bias and relativistic satellite clock corrections.

$Tr_{d}$ is a non-dispersive delay caused by tropospheric layer.

$ION_{d}=\alpha STEC$ is infrequency-dependent delay caused by ionospheric layer. Where $STEC$ is the electron density along the ray path of a GNSS ranging signal and $\alpha$ is the conversion factor between the $STEC$ and the estimated signal delay at frequency $f$.

$Rcv_{d}$ is receiver instrumental delay that is dependent on code and frequency.

$Sat^{i} _{d}$ is satellite instrumental delay of satellite $i$ that is dependent on code and frequency.

$M_{d}$ is the delay caused by multipath and is dependent on code and frequency.

$Offset^{i} _{ant}$ is the geometric offset (distance) between a satellite and its antenna phase centre (APC).

$\varepsilon _{rcv}$ is the noise of a receiver.

From equation 3, we can observe that, the travel time of a ranging single from an emission time to a reception time is complex. There are a lot of factors that cause the variations (in this case delay) of the travel time of the ranging signals.

These variations directly affect the accuracy and precision of estimated pseudorange. Meaning, these factors are significant or relevant uncertainty contributors for pseudorange, and hence, GNSS positioning.

Carrier phase (carrier) pseudorange measurement

Pseudorange calculated from carrier phase measurement is more precise than the one obtained from code measurement.

However, carrier phase measurement inherently contains ambiguity by “unknown” integer multiple of the carrier wavelength ($\lambda N$).

The pseudorange of carrier phase measurement is formulated as:

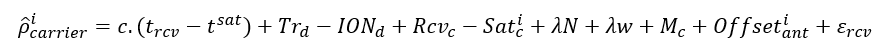
Where:

$Rcv_{c}$ is receiver instrumental delay that are dependent on frequency.

$Sat^{i} _{c}$ is satellite instrumental delay of satellite $i$ that is dependent on frequency.

$M_{c}$ is the delay caused by multipath and is dependent on frequency.

$\lambda$ is the carrier wavelength.

$N$ is the (unknown) integer ambiguity that should be estimated.

$\lambda w$ is wind-up effects caused by electromagnetic signal’s circular polarisation.

As we can see from equation 4, there is a fundamental difference between code and carrier phase pseudorange calculations.

That is, carrier phase pseudorange contains integer ambiguity. This ambiguity if not known, can lead to up to thousand of kilometre calculated position bias (systematic error).             

In addition, one particular aspect we can notice is that ionospheric layers advance the carries instead of delaying the carrier as opposed to the code pseudorange calculation.

It is worth to note that ionospheric delay is quite a hot topic in research activities with the aims to estimate the total electron content (TEC) in areas to estimate and compensate the ionospheric delay. Recent methods to predict TEC in areas are by using dep neural network and its derivations [4,5].

Satellite clock bias also causes pseudorange errors since the GNSS timeline deviates from its true timeline due to in the internal bias of on-board atomic clock. Recent work implements a transformer deep neural network to predict satellite clock-bias for up to two hours along the future horison time [6].

READ MORE: Brief discussions on uncertainty contributors of GNSS-based positioning (Part 1)

Combination of GNSS measurements

For precise point positioning (PPP), Combinations of pseudorange measurement, typically at different frequencies, are needed.

These combinations can improve the accuracy and precision of pseudorange measurement by for example, eliminating factors affecting the ranging signal travel time, such as ionospheric delay.

Several GNSS pseudorange measurement combinations are [3] (where $i=1,2$ are indication of using $f_{1}$ and $f_{2}$):

• Geometric free combinations:

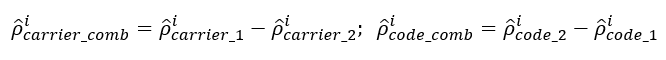
This combination cancels the geometric variables in the pseudorange calculation and leave only frequency dependent variables, such as ionospheric delay, instrumental delays, etc).

• Ionosphere-free combinations:

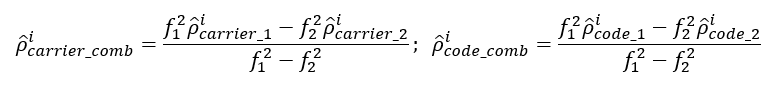
This combination removes the ionospheric effect (first order, up to 99.9%).

• Wide-Lanning combinations:

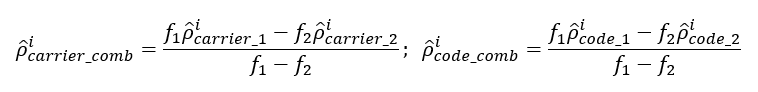
This combination forms a measurement with a very long wavelength in order to detect cycle-slip and fixing ambiguities.

• Narrow-Lanning combinations:

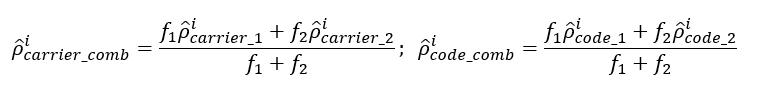
This combination forms a measurement with very low noise.

Receiver noise and multipath

The effect of receiver noise (equation 3 and 4) to the code measurement is commonly about 1% of a single chip [3]. For example, for GNSS signal with 1.023MHz code rate, this receiver noise is translated to approximately 3m pseudorange error ($1%$ of $1 chip$ for $1 \mu s$ = $1% \times 300m$).

Meanwhile, for the carrier measurement, the receiver carrier phase noise is also about 1% of the carrier phase wavelength and is translated to few mm of pseudorange error.

Regarding the effect of multipath to pseudorange error [3], for code pseudorange measurement, typically is around 3m. However, theoretically the effect of multipath error to the code pseudorange error can be up to o 450m (1.5 chip of GPS L1 or GAL E1).

But, the power of this multipath signal will typically be very low (compared to the line-of-sight signal) and can probably may not be observed.

For the carrier pseudorange measurements, the multipath error effect is typically $<1cm$. However, theoretically, the carrier pseudorange error will be a quarter of the wavelength and is translated to about $5cm$.

Form here, we can see that the carrier pseudorange measurement is more robust than code pseudorange measurement.

READ MORE: Measurement uncertainty estimation: Spreadsheets method

Uncertainty contributors for pseudorange measurements

From the above discussions, we can see that there are a lot of factors that significantly affect the calculation of pseudorange measurements. Those factors are then relevant uncertainty contributors for pseudorange measurements.

Those variables affecting the code pseudorange and carrier phase pseudorange measurements can be eliminated/compensated or substantially minimised by using combination of measurements (from difference GNSS signals at different frequencies and/or constellation).

However, there are other variation factors that are not explicitly shown in the equation and cannot be compensated or eliminated by multiple combination of measurements but affect both code and carrier phase pseudorange measurements.

These variations factors are analog-to-digital system used in a receiver, the power of GNSS signals, the correlation process between the GNSS signal and local replica and other factors. These factors affect the signal processing process of GNSS signals.

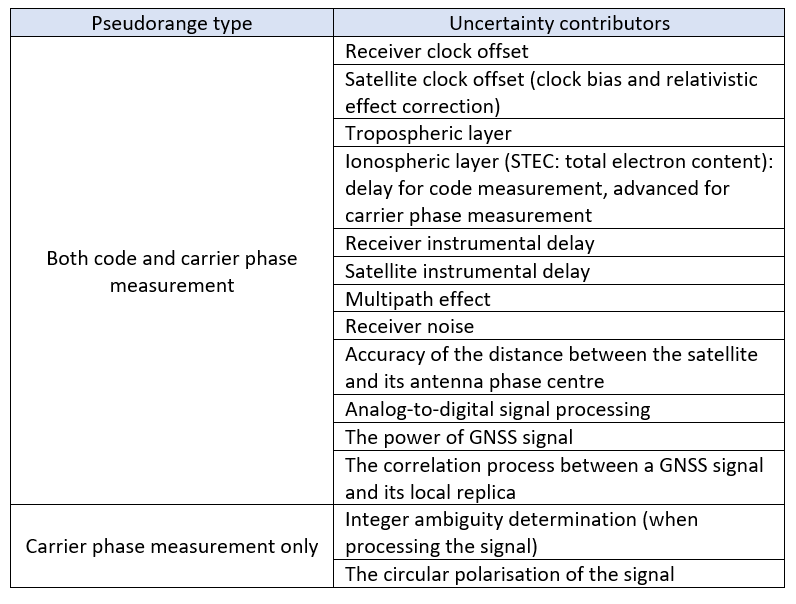
Finally, table 1 shows the summary of factors affecting pseudorange measurements. In this table, more detailed uncertainty contributors are separated based on the type of pseudorange measurement the contributors are relevant to.

READ MORE: GPS (GNSS) signal processing chain from a received raw signal, signal acquisition, tracking to demodulation: An introduction

Conclusion

Factors affecting the formation of pseudorange between a GNSS satellite and a receiver have been discussed in this post.

There two main methods in calculating pseudorange: by code measurement or by carrier phase measurement. Pseudorange calculated from code measurement is noisy but unambiguous. Meanwhile, the one obtained from carrier phase measurement is precise but contain ambiguity leading to pseudorange bias.

To improve the accuracy and precision of pseudorange measurements, combination code and carrier phase measurements at different frequencies can be implemented.

Finally, more detailed uncertainty contributors specifically that are relevant to pseudorange are summarised.

Reference

[1] Kaplan, E.D. and Hegarty, C. eds., 2017. Understanding GPS/GNSS: principles and applications. Artech house.

[2] P. Misra and P. Enge. 2006. “Global Positioning System: Signals, Measurement and Performance.” 2nd edition.

[3] J. S. Subirana, J. M. J. Zorboza, M. Hernandez-Pajarez (2013). GNSS data processing. Volume 1: Fundamentals and algorithm. European Space Agency (ESA).

[4] Priyadarshi, S., Syam, W.P., Roqué, A.A.G., Conesa, A.P., Buscarlet, G., Pérez, R.O. and Orso, M.D., 2023, September. High-solar Activity Ionospheric Modelling Using Machine Learning: A comparison Against Classical Models. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023) (pp. 121-135).

[5] Priyadarshi, S., Syam, W., Roqué, A.A.G., Conesa, A.P., Buscarlet, G., Pérez, R.O. and Orso, M.D., 2023, January. Machine Learning-based ionospheric modelling performance during high ionospheric activity. In Proceedings of the 2023 International Technical Meeting of The Institute of Navigation (pp. 950-965).

[6] Syam, W.P., Priyadarshi, S., Roqué, A.A.G., Conesa, A.P., Buscarlet, G. and Orso, M.D., 2023, January. Fast and reliable forecasting for satellite clock bias correction with transformer deep learning. In Proceedings of the 54th Annual Precise Time and Time Interval Systems and Applications Meeting (pp. 76-96).

 You may find some interesting items by shopping here.