Brief discussions on uncertainty contributors of GNSS-based positioning (Part 1)

In this blog series, we will discuss about uncertainty contributors on GNSS positioning and open a way to estimate the uncertainty for reliable positioning.

The accuracy of a position calculated from global navigation satellite system (GNSS) ranging signals becomes more and more important than ever [1,2,3].

The reason is that, today applications, for example, mobile navigation mapping (satnav), autonomous driving, precision agriculture and others, require high accuracy and also reliable positions [4].

GNSS positioning can be said to be reliable only if the measurement uncertainty of the positioning is provided, that is, estimated.

Many misunderstandings about uncertainty think that this uncertainty is only a simple standard deviation of repeated measurements or only estimation of dilution of precision.

Uncertainty is more beyond these values.

In this blog series, we will start the discussion from the basic traceability and uncertainty discussions, including GUM method until various uncertainty contributions for GNSS positioning.

Traceability is a property of a measurement that can be traced back to a “reference” unit.

Note that, the are arguments regarding traceability in that all the seven basic units are only completely relevant inside the earth. Meanwhile, GNSS system involves physical and chemical processes outside the earth (space).

In our discussion, we will consider that all the seven basic units are still completely relevant for both inside the earth and space.

READ MORE: The fundamental concept of metrology

Principle of metrology: Traceability

In metrology, the main discussion is always around traceability.

When a measurement result is traceable, it means that the measurement can be traced back or connected to the one or several basic unit definitions. For example, for a length, distance or size measurement, the reference unit is the metre definition.

Traceability is tightly coupled and always goes hand-in-hand with calibration and uncertainty. Figure 1 below illustrates this interconnection among traceability-calibration-uncertainty.

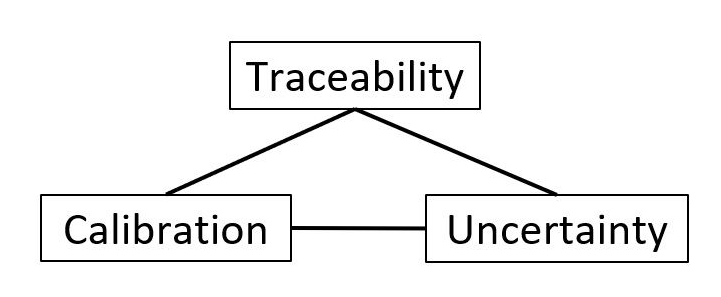
The reference definitions of these three terms: traceability, calibration and uncertainty are defined in JCGM:2012 VIM [5] as follows:

• Traceability (metrological traceability): “Property of a measurement results whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty” [5].

In short: each measurement should link to another higher accuracy measurement and so on until the link reaches the definition of the unit.

• Calibration: “Operation that, under specified conditions, in a first step, establishes a relation between the quantity values with measurement uncertainties provided by measurement standards and corresponding indications with associated measurement uncertainties and, in a second step, uses this information to establish a relation for obtaining a measurement result from an indication” [5].

In short: a process to compare the result of a measurement with another measurement result at higher accuracy and to estimate the uncertainty of the measurement result.

• Uncertainty (measurement uncertainty); “Non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information used” [5]. Measurand is a quantity intended to be measured.

In short: the value range of a measurement result where the true value is believed lies in between. Uncertainty is estimated from a calibration process.

READ MORE: Measurement uncertainty estimations: GUM method

Traceability of GNSS positioning

GNSS position measurement is basically a length measurement since the measurement presents a quantity measured in unit length (km, m, or cm).

In addition, the GNSS positioning is also tightly coupled with time measurement (receiver clock bias) as well as time of flight of GNSS signals from satellites to a receiver.

Hence, although the positioning is defined in unit length, the time factor is critical in GNSS positioning calculation and hence, traceability to unit time (second) is also relevant.

This aspect causes another problem and debate. That is, since GNSS system involve phenomenon both inside the earth and space, the common traceability property of GNSS positioning may not 100% relevant.

There are debates that when the phenomena happen in space, the traceability chain can be broken. For example, the physical phenomena that defines time may not behave equally when it is in space, for example, the relativistic effect become relevant in space (and not the case for in eart).

Following JCGM:2012 VIM, the definition of metre and second are as follows:

• The metre definition is the length of a path travelled by light in a vacuum for 1/299792458s duration. This definition is valid for condition within the earth and space.
• The second definition is the duration of 9192631770 of radiation period due to the transition between two hyperfine levels from Caesium 133 atom. This definition may or may not be the same in the space environment.

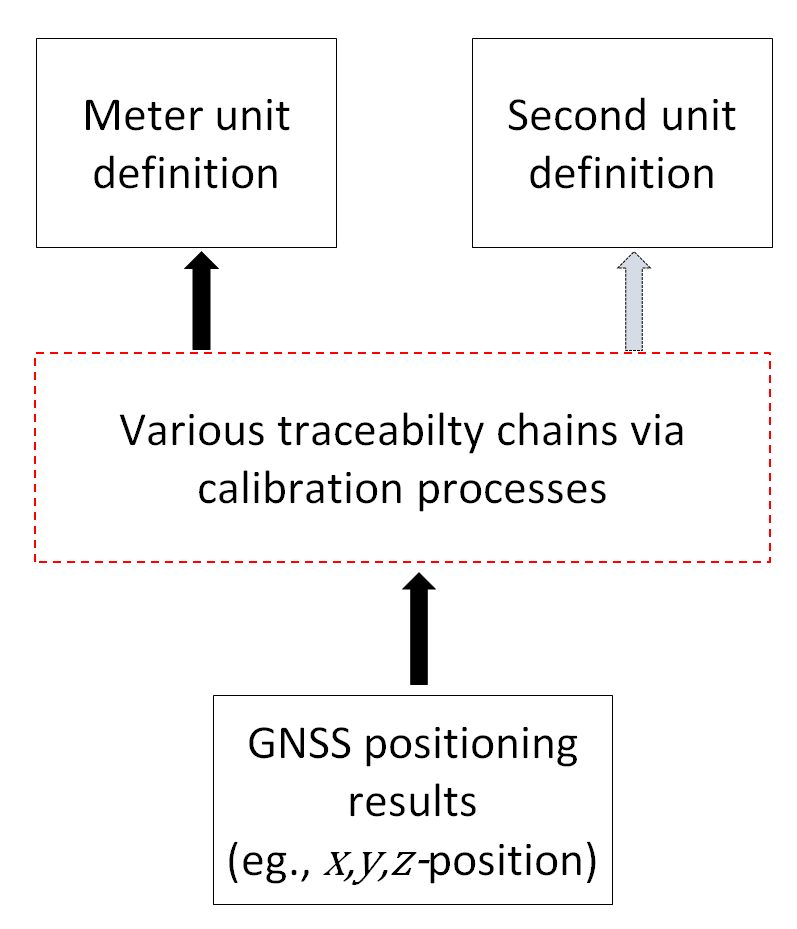
Figure 2 shows the illustration of the traceability chain of GNSS positioning measurements. In figure 2, the traceability stops at the metre and time definitions. Although the primarily traceability will be to the metre definition, if one of the calibration processes involves timing, then the traceability also goes to the second definition.

READ MORE: GPS (GNSS) signal processing chain from a received raw signal, signal acquisition, tracking to demodulation: An introduction

Uncertainty estimation of measurement results

Uncertainty is necessary to representing a final measurement to be deemed reliable and to show the traceability of a measurement [6].

In general, a reliable or complete measurement result presentation is as follows (just an example):

• The position of a receiver is at $(X+\pm Ux, Y+\pm Uy, Z+\pm Uz)$ location.
• The interval value (uncertainty) is the expanded uncertainty of 95% with $k=2$ (assuming normal distribution on the data).
• The interval value (uncertainty) is calculated considering uncertainty contributors of ionospheric effect, tropospheric effect, etc. and from 10 repeated measurements.

The reference method to estimate measurement uncertainty is GUM method. In this method, all uncertainty contributors $X_{i}$ are all propagated into the final measurement $Y$.

The GUM method to estimate the uncertainty $u(Y)$ of measurement $Y$ is formulated as [6]:

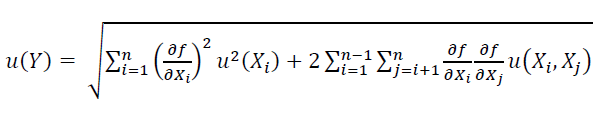
Where:

• $u(Y)$ is the total standard uncertainty value of a measurement $Y$ propagated from its contributing factors $X_{i}$.
• $X_{i}$ is $i-th$ contributor to the uncertainty.
• $u(X_{i},X_{j})$ are the correlation values between contributors $X_{i}$ and $X_{j}$

Commonly, uncertainty is presented within 95% confidence interval and is called as expanded uncertainty $U$ (assuming normal distribution on the measurement data).

$U$ is formulated as (assuming Gaussian or normal distribution):

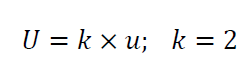
However, the main drawback of this method is that this method requires we have the mathematical measurement model that is “algebraically continuous”. That is, the measurement model can be mathematically derived (mathematically tractable).

In many situations, many measurement results are obtained from a complex underivable equation (non-continuous). This complex equation is commonly solved by an approximation and/or iterative algorithm, such as in the case of GNSS positioning calculation [7].

Furthermore, there are situations where the mathematical model of measurements is not known.

In the next post, we will see how the GNSS positioning is calculated and discuss the difficulty of implementing GUM method to estimate the uncertainty of GNSS positioning.

For situations where the GUM method is difficult to apply, alternative methods, that are practical to most cases, are available, that are spreadsheet method or Monte-Carlo method.

READ MORE: Measurement uncertainty estimation: Spreadsheets method

Conclusion

In this post, we have started a series of discussions about the traceability ad uncertainty contributors for GNSS positioning measurements.

The traceability of GNSS positioning is discussed to relate all GNSS positioning measurements to unit metre definition (length) as well as unit second definition (time).

However, there are arguments about whether the current traceability is completely relevant since GNSS systems also involve physical and chemical phenomenon in space as well as inside the earth.

Particularly, this post starts the discussion on what traceability and measurement uncertainty are and what the reference method to estimate or determine a measurement uncertainty is.

Reference

[1] Kaplan, E.D. and Hegarty, C. eds., 2017. Understanding GPS/GNSS: principles and applications. Artech house.

[2] P. Misra and P. Enge. 2006. “Global Positioning System: Signals, Measurement and Performance.” 2nd edition.

[3] J. K, Holmes 2007 Spread spectrum systems for GNSS and wireless communications. Norwood, MA: Artech House.

[4] F. Van Diggelen. 2009. “A-GPS: Assisted GPS, GNSS, SBAS”.

[5] JCGM 200:2012 International Vocabulary of Metrology - Basic and general concepts and associated terms (2012)

[6] JCGM 100:2008(E), Evaluation of measurement data - Guide to the expression of uncertainty in measurement (2008).

 [7] J. S. Subirana, J. M. J. Zorboza, M. Hernandez-Pajarez (2013). GNSS data processing. Volume 1: Fundamentals and algorithm. European Space Agency (ESA).

You may find some interesting items by shopping here.