GNSS

Brief discussions on uncertainty contributors of GNSS-based positioning (Part 4)

Satellite orbit, the last main components required to calculate GNSS-based positioning, will be discussed in this post as well as the uncertainty contributors that are relevant to the satellite orbit estimation.

Wahyudin Syam

Apr 27, 2024 • 8 min read

Variables used to calculate the satellite orbit of GNSS satellites are presented along with the calculation formulas. These variables are decoded from GNSS navigation messages.

The variables decoded from the navigation messages are called “satellite Ephemeris” then processed (calculated) to estimate the satellite orbit or position.

The term “ephemeris” is obtained from celestial navigation and represents the trajectory of astronomical objects (the Moon, Sun, stars and others) as well as artificial or man-made satellites.

Note that the ephemeris of GNSS satellites is updated from a master ground station on Earth. The update of the ephemeris is periodical. For example, in GPS satellites, their ephemeris is updated every two hours [1,2].

In this post, we will start from a brief discussion on coordinate system and then satellite orbit determination. Finally, the uncertainty contributors of satellite orbit estimations are discussed.

Coordinate systems

There are several coordinate systems where a coordinate of point or location refers to. The use of these various coordinate system depends on applications.

Basically, all applications can use any coordinate systems. However, in many cases, there a more straightforward coordinate system compared to other systems for each application.

There are two main coordinate systems that are commonly used: Earth-Centre-Erath-Fixed (ECEF) coordinate system (Cartesian system) and Geodetic (ellipsoidal) coordinates system (Long, Lat, Attitude).

For the antenna phase centre of GNSS satellites, these phase centres are related to specific geodetic coordinates systems. For example, for GPS, the antenna phase centre is defined based on WGS84 coordinate system, for GALILEO, the antenna phase centre is based on Galileo Reference Frame (GTRF), for GLONASS, the antenna phase centre is related to PZ-90 coordinate system and BEIDOU is related to BEIDOU Reference System CGCS2000 [3].

Earth-Centred-Earth-Fixed (ECEF) coordinate system

The ECEF system is the most common coordinate system used in many applications. The ECEF reference system is fixed at the earth centre and follows the rotation of the earth.

The notation for coordinate in ECEF is as $(x,y,z)$ coordinates.

The advantages of ECEF coordinate system are that it is a straightforward system, is computationally efficient and easy to calculate distance between two points within the coordinate system.

However, the main drawback of this coordinate system is that the coordinate system is not geographically intuitive.

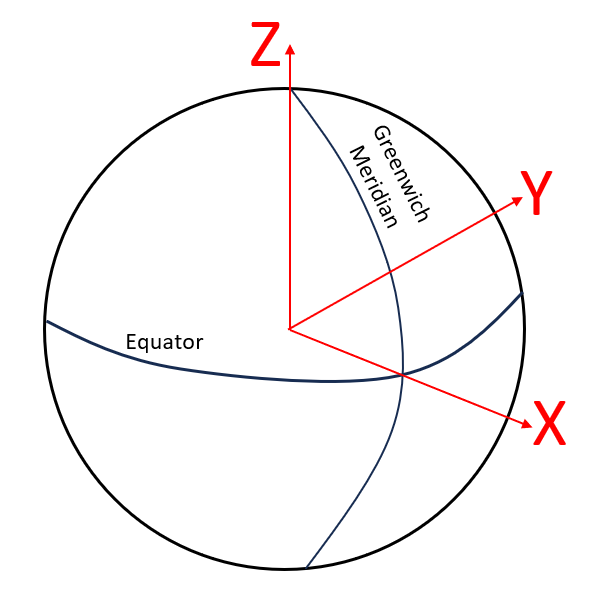
Figure 1 below shows the schematic view of the ECEF coordinate system. From this figure, the centre of the ECEF is coincident with the earth centre point, the X-axis passes through the intersection point between the equator and Greenwich meridian and the system follow the right-hand rule.

Figure 1: The schematic view of ECEF coordinate system.

Geodetic Coordinate System

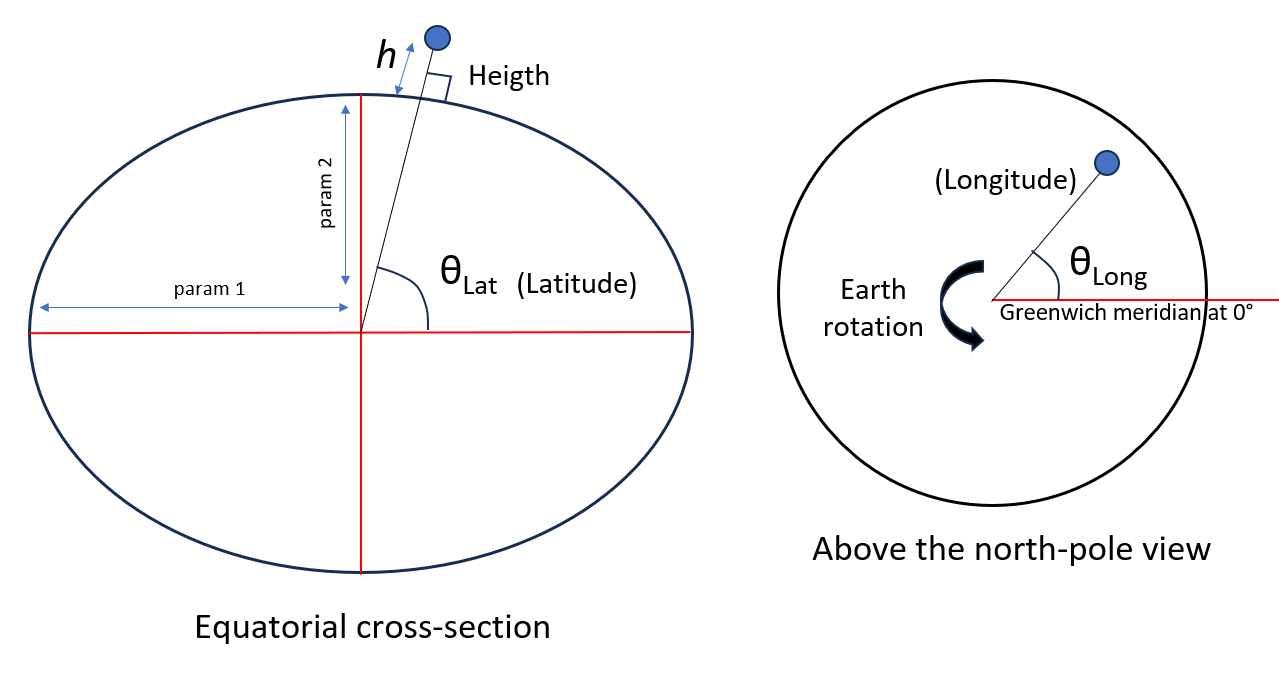
Geodetic coordinate system follows the definition of ellipsoid. Figure 2 below illustrates the geodetic coordinate system.

The notation for coordinate in geodetic system is as $(Longitude (Lon), latitude (lat), height (h))$ coordinates.

The longitude is the angle of a location with respect to a horizontal line of the world viewed from the north pole. Meanwhile, the latitude is the angle of the position with respect to a horizontal line with respect to the Earth cross-section at the equatorial (Figure 2).

And the height (typically expressed in metre) is the height of a location orthogonal to the surface of the Earth on that location.

Figure 2: The illustration of geodetic coordinates system.

Especially for longitude and latitude, they can be expressed in different ways, that are:

Radian

Although this representation is not geographically intuitive, this representation is straight forward and can be used in computational programming.

Decimal degree

This representation is directly intuitive for human and can be easily converted form radian to decimal degree. Sometimes, the decimal degree only representation can lead to no-integer value, for example 45.57 degree.

Decimal degree along with decimal minutes

To represent the decimal degree in integer, the fractional degree is represented in minutes where 1 minutes = 1/60 degree. For example, 45.57 degree = 45 degree, 34.2 minutes.

Decimal degree, minute, second

To represent the decimal degree and minutes in integer, the fractional minutes is represented in second where 1 second = 1/60 minute. For example, 45.57 degree = 45 degree, 34 minutes, 12 seconds.

Satellite orbit or position calculations

The orbit or location of GNSS satellites in ECEF coordinate system are calculated from their broadcasted ephemeris. These ephemerides are obtained from the navigation messages decoded from the GNSS signals.

In this post, the computation of satellite orbit for GPS, GALILEO and BEIDOU are presented since these constellations have the same ephemeris parameters and orbital computation methods [3]. GLONASS has a different orbital computation. However, the idea is the same. That is, computing satellite orbits are performed from their broadcasted ephemeris.

Ephemeris parameters (for GPS, GALILEO, BEIDOU):

The list of ephemeris parameters used by GPS, GALILEO and BEIDOU systems are as follows (GLONASS has different ephemeris parameters) [3]:

Parameters to define orbit shape and timing:

$t_{OE}=$ Ephemeris reference epoch in seconds of week /$s$.

$\sqrt{a}=$ Square-root of semi major axis /$\sqrt{m}$.

$e=$ Eccentricity.

$M_{0}=$ Mean anomaly at reference epoch /$rad$.

Parameters to define orientation/position of orbit:

$\omega =$ Argument of perigee at $t_{0}$ /$rad$.

$i_{0}=$ Inclination of reference epoch at $t_{0}$ /$rad$.

$\Omega _{0}=$ Longitude of ascending node at $t_{0}$ /$rad$.

Parameters for correction terms:

$\Delta n=$ Mean motion difference or correction /$rad/s$.

$\dot{\Omega} =$ Rate of change of $\Omega$ /$rad/s$.

$\dot{i} =$ Rate of inclination angle /$rad/s$.

$C_{UC}, C_{US}=$ Latitude argument correction coefficient.

$C_{RC}, C_{RS}=$ orbital radius correction coefficient.

$C_{IC}, C_{IS}=$ Inclination correction coefficient.

Parameters of satellite clock offset:

$a_{0}=$ Satellite clock offset.

$a_{1}=$ Satellite clock drift.

$a_{2}=$ Satellite clock rate.

These variables will be used to compute the orbit or location of a GPS/GALILEO/BEIDOU GNSS satellite.

Computations of satellite orbit or coordinate (for GPS, GALILEO, BEIDOU):

The steps to compute the satellite orbit is as follows:

Compute the time $t_{k}$ from the $t_{0}$ of the reference epoch for the ephemeris:

equation 1

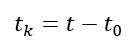
Note that $t$ and $t_{0}$ are in GPS week second.

Compute the mean anomaly at $t_{k}$:

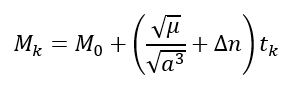
Compute (iteratively solve) the Keppler equation for $E_{k}$ eccentric anomaly:

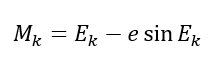
One way to solve the Kepler equation iteratively is by using Newton’s iterative method as follows:

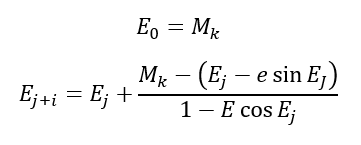
Compute the true anomaly $v_{k}$:

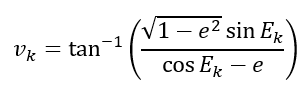
Compute the latitude argument of $u_{k}$:

equation 6

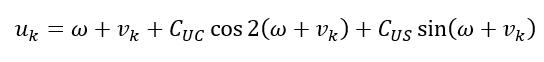
Compute the radial distance $r_{k}$:

equation 7

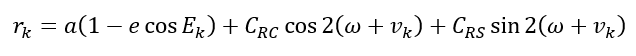
Compute the orbital plane inclination $i_{k}$:

equation 8

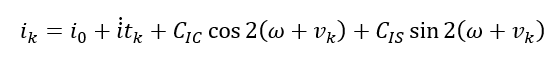
Compute the ascending node longitude $\lambda _{k}$. This ascending node is with respect to Greenwich:

equation 9

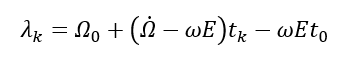
Compute the satellite coordinate in ECEF frame (coordinate system):

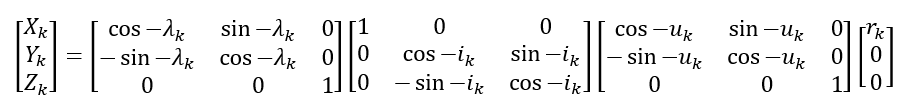
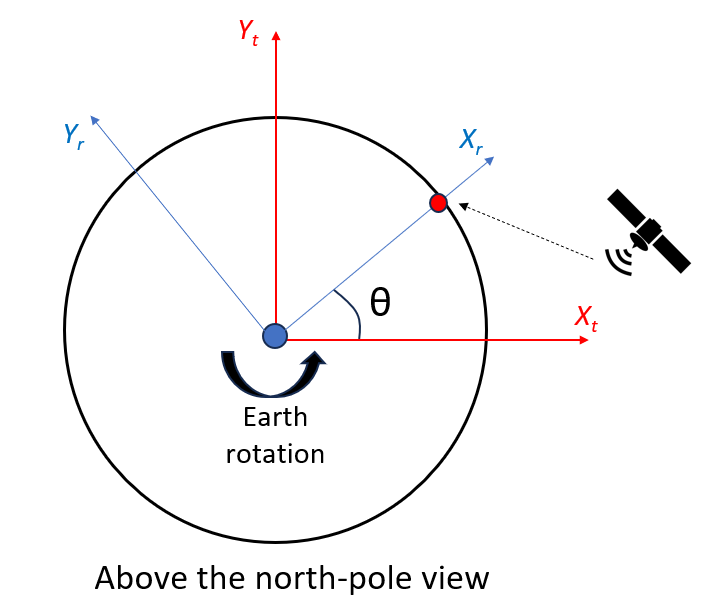
Finally, since during signal transfer, the receiver position is rotated due to the earth rotation, we should also consider the effect of the Earth rotation after a signal is transmitted from a satellite and then received by a receiver as follows (see figure 3 below):

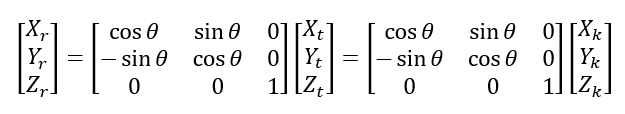
Where:

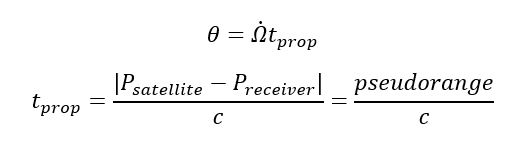
The explanation of the equation above to consider the Earth rotation as shown in figure 3 below. In figure 3, the “t” denotes “at transmit time” and “r” denotes “at receive time”.

Figure 3: The illustration of the relation of satellite position at receive time with respect to satellite position at trasmit time due to the Earth rotation.

Uncertainty contributions on Satellite orbit or positions calculations

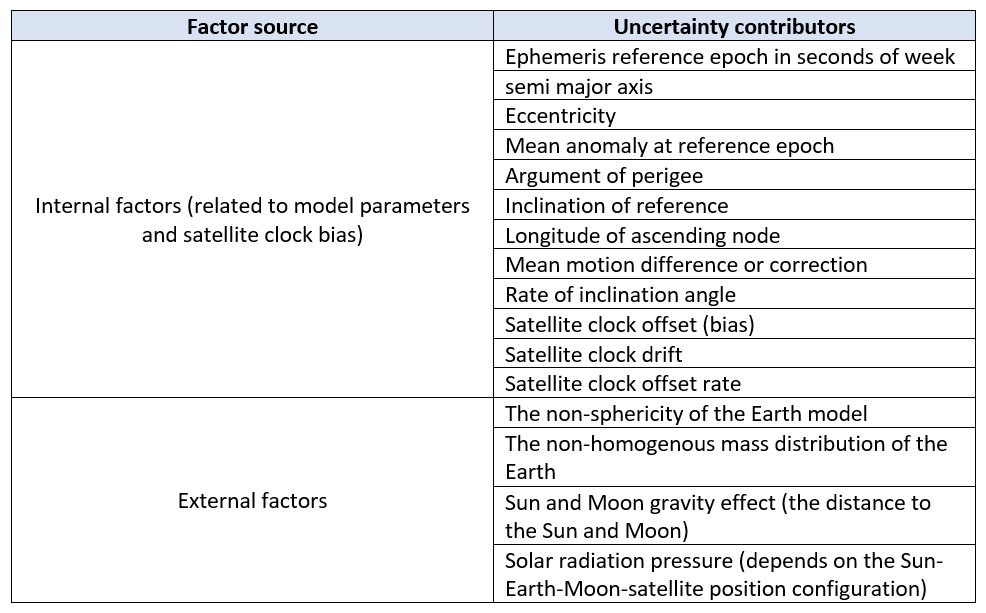
From the variables of the equations to calculate the orbit of GNSS satellites, relevant uncertainty contributors for satellite orbit or location can be directly derived from these variables.

In general, these relevant variables, used to calculate the orbit of the satellites, depend on the dynamic of the satellite. The dynamics of the satellite are affected by both external factors and internal factors [3][4].

Th external factors affecting the satellite dynamic are the non-sphericity and non-homogeneous mass distribution of the Earth, the Sun and Moon gravity effect [4], solar radiation pressure and others (depends on the Sun-Earth-Moon-satellite position configuration [4]). These external factors will perturb the satellite motion and then deviate from its expected position.

Meanwhile, the internal factors affecting the satellite dynamic are satellite clock bias, the model of the satellite orbit determination and the satellite orbit update process.

Table 1 summarised the relevant uncertainty contributors for satellite orbit determination. The ephemeris reference epoch is directly affected by the clock bias of a GNSS satellite. Because the satellite clock bias will cause the real time epoch to deviate from its nominal.

Table 1: The summary of uncertainty contributors for satellite orbit determination.

Conclusion

Satellite orbit is one of the instrumental variables in navigation equation to derive the location of a GNSS receiver. In this post, we discuss what are those relevant uncertainty contributors of satellite orbit estimation.

The uncertainty contributors come from both internal factors and external factors.

The internal factors are those variables used in the model for satellite orbit determination as well as satellite clock bias.

Meanwhile, the external factors are variables that depend on external phenomenon, such as the Sun-Moon-Earth-Satellite configuration and the distance of a satellite to the Sun and Moon.

Finally, the steps to estimate the orbit or coordinate (in ECEF) of GNSS satellites are presented.

Reference

[1] Kaplan, E.D. and Hegarty, C. eds., 2017. Understanding GPS/GNSS: principles and applications. Artech house.

[2] P. Misra and P. Enge. 2006. “Global Positioning System: Signals, Measurement and Performance.” 2nd edition.

[3] J. S. Subirana, J. M. J. Zorboza, M. Hernandez-Pajarez (2013). GNSS data processing. Volume 1: Fundamentals and algorithm. European Space Agency (ESA).

[4] Syam, W.P., Priyadarshi, S., Roqué, A.A.G., Conesa, A.P., Buscarlet, G. and Orso, M.D., 2023, September. Transformer deep learning for accurate orbit corrections in real-time. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023) (pp. 159-174).

You may find some interesting items by shopping here.