Calculus and linear algebra as tools for statistics
Very often, statistics is overlooked by engineers and the importance of statistics is put behind calculus and (linear) algebra.
Very often, statistics is overlooked by engineers and the importance of statistics is put behind calculus and (linear) algebra. In undergraduate program in university, for example in engineering, statistics courses are only given a fraction of credits from the total credits for engineering studies. That is, commonly statistics only provided in two courses or modules (if not one course or module only) within the average four-year engineering undergraduate program.
In addition, only descriptive statistics and few inferential statistics are thought in engineering undergraduate program, such as how to determine mean and variance from normal distribution and to make statistical test, such as t-student test. However, statistics are much more than that, such as there are many types of statistical distributions, many types of method to fit statistical distributions, many types of statistical test, many types of statistical parameter fitting methods and many more.
In fact, in real world problems, the problems are always stochastic instead of deterministic. Stochastics means that the problem is suitably described by using random probability distributions. That is, there is uncertaintyinvolved in the data and output of the problems.
To analyse, characterise and estimate these randomness and uncertainty of the real-world problems, statistics is required. Statistics should be used to model the problems so that we can make prediction and analysis of the problems through the developed statistical models.
Especially in all scientifical fields, from science, engineering, medicine, economics to social sciences, all data or measured quantity values have uncertainty, that is the value is not deterministic and always changed when the values are re-measured.
Hence, statistics is very important and should be considered as the same priority as other mathematical fields such as calculus and linear algebra.
Next, we will discuss just few (out of much more) examples why statistics needs the understanding of calculus and linear algebra.
Let us go into the discussion!

Examples on how important statistics is to model real-world problems
As mentioned before, many real-world problems are stochastic and involve uncertainty in their data. Hence, statistics is the best tool to model and study the problems and make effective solutions.
Some examples of real-world problems that require statistics are:
- Uncertainty estimation of measurement results. All measurements, from parts, fluids, disease, census and other types of measurement have uncertainty that represents a range (variation) in which the true measurement value lies in between. Only by estimating the uncertainty, the measurements are considered as reliable and comparable.
- Discrete industrial system analysis. In discrete industrial system, such as production processes, all data contain variations that need to be considered and characterised to study the processes. Statistics can model and characterise the variations to understand the processes well.
- Resource assignment problem analysis. Examples of these type of problems are gate assignment in airport and other similar types of problems. The arrival time of each plane is not exact, instead they are stochastic and contain variations.
- Scheduling and queuing system analysis. In real-life, we need to schedule everything, from university exams to computer task scheduling. For example, in computer scheduling, each task processing time will be vary, depending on the load of the processor and memory as well as data channel communication speed.
- Parameter fitting. In any scientific field, including medicine and social science, many times we need to fit the parameters of a model, representing a problem at hand, so that we can use the model for prediction and analysis.
- And many other real-world problems.
READ MORE: The most important tools for research
Examples on how calculus and linear algebra are as tools for statistics
The calculation of expected values (means, variance) requires integral operation
The basic statistics is to calculate the mean and variance from data. The general form of calculating the mean and variance of any types of statistical distributions are as follow [1,2,3]:
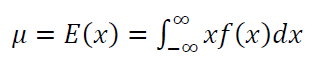
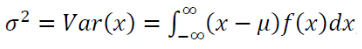
Where $\mu$ and $\sigma ^{2}$ are the mean the variance. As we can see from the equations, to calculate the mean and variance, we need to use integral operator from calculus field.
The least-square fitting requires linear algebra
Least-square fitting is the most common criteria to estimate the parameter of a model [2]. For example, the most common statistical model is linear regression.
The general model of linear regression is as follow:
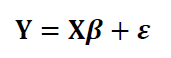
Where:
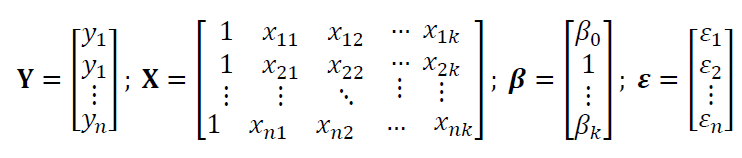
The least-square fitting method is performed as follow:
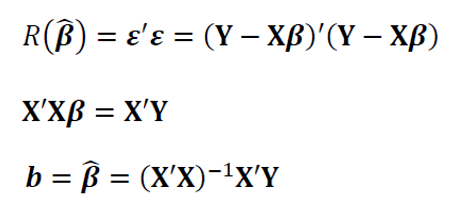
Form the equation above, we can see that the variables are in matrix forms and require the knowledge of linear algebra to solve the normal equation and to estimate the model parameter $\beta$.
Least-square fitting is like maximising maximum likelihood
Continuing the least-square fitting method above, basically least-square fitting is the process of minimising the sum-of-square error function:
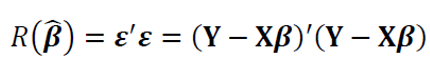
The minimisation of the sum-of-square error above, from the probabilistic point of view, is equal to the maximisation of the log-likelihood function under Gaussian noise distribution as follow [1]:
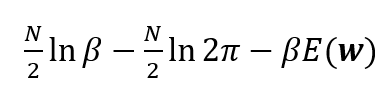
To be able to minimise the equation above with respect to $\beta$ and $w$, we need to use derivation operator (gradient) applied to vector variables. These processes require the knowledge of calculus and linear algebra at the same time.
READ MORE: The most important tools for research
- Grammar Rules: Everything you need to know but never learnt in school – A book about how to make efficient and concise sentences to writing with military precision!
Time series analysis
Time series analysis is different with common interpolation method. Time series analysis is the analysis of data that are collected sequentially over-time [3].
Time series analysis is considered as extrapolation problem. Because we only interest to predict the future and not the past (as the past never happen again).
There are many models for time-series data, such as auto regressive (AR), moving average (MA) and the combination of both [3]. To estimate the parameter of these model, we need to applied model fitting.
Consider the simplest time-series model, that is MA(1), the model is:
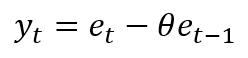
Where $e$ is the error, $\theta$ is the model parameter and $t$ is time index. The equation above requires a statistical fitting method, such as least-square fitting, to estimate the model parameter $\theta$
Machine learning: a new name for statistics
Of course, everybody knows about machine learning (ML) nowadays. Because ML is mentioned everywhere and used almost everywhere. We can hardly avoid this buzz word!
However, basically the famous ML methods are basically statistics [1]. Inside ML, there are least-square fitting, matrix algebra, gradient descent calculus, statistical distribution parameter fitting, model optimisation, and many other statistical processes.
Hence, if we can understand the importance and the power of ML, then automatically we will understand the importance and power of statistics.
READ MORE: Is research expensive?
Conclusion
In this post, the important of statistics and why we should put special attentions to statistics as it deserves have been explained. Statistics should be viewed as importance as other mainstream mathematical fields, such as calculus and (linear) algebra.
Most of real-life problems are stochastics instead of deterministic and involve uncertainty in the data and outputs. To model these real-life problems, statistics is required to model and characterise the problems and data.
However, statistics requires calculus and algebra to develop, analyse and fitting the model parameters from data so that the model becomes useful for prediction and analysis. And hence, making insights and solutions for the problems. There are few examples to show the role of calculus and linear algebra as tools for statistics. But there are much more cases where calculus and linear algebra are needed to support statistics.
References
[1] Bishop, C. M. (2006). Pattern recognition and machine learning (Vol. 4, No. 4, p. 738). New York: springer.
[2] Montgomery, D. C. (2017). Design and analysis of experiments. John wiley & sons.
[3] Cryer, J. D., & Chan, K. S. (2008). Time series analysis: with applications in R (Vol. 2). New York: Springer.
You may find some interesting items by shopping here.
