The role of measurement uncertainty in quality inspection
In quality inspection, measurement uncertainty has a fundamental role in deciding the conformance and non-conformance of a part.

In quality inspection, measurement uncertainty has a fundamental role in deciding the conformance and non-conformance of a part.
Not only for measurement traceability, but also for quality inspection processes, measurement uncertainty needs to be considered to determine whether a part conforms to its specification or not.
Without measurement uncertainty statement, the conformance and non-conformance decision of a part, in a quality inspection process, cannot be made.
In this post, the reason for why measurement uncertainty is required in quality inspection processes is explained and detailed quantitative examples are given as a case study.
With the detailed examples, the role of measurement uncertainty in the inspection processes is quantitively explained.

How can measurement uncertainty affect conformance and non-conformance decisions in quality inspection?
In reality, it is very often there is a situation where a company send a part that passes its internal quality inspection process. But then, the part is rejected by another company who purchases the part because the part does not pass the company (the purchaser) incoming quality inspection.
In this situation, a legal intervention will be performed and very often they end up in a court. Because, in many situation the part that has been made has a very high production cost. And, this cost should be paid by one of the companies (the producer or purchaser) to be able to pay the salary of workers involved in the part’s production processes.
Measurement uncertainty has its critical role in preventing and solving this kind of disputing situation between companies.
In legal metrology, how the conformance and non-conformance of parts are decided between a seller and buyer is by stating how the conformance decision is made by considering the measurement uncertainty of the part.
Without stating the measurement uncertainty of a measurement result, the measurement result cannot be used to take the decision to accept or reject a part in quality inspection.
The next section will present a case study as quantitative example of how a measurement uncertainty has a critical role in a disputing situation between two companies.
A quantitative example on how to consider uncertainty in quality inspection
In this example, a case between two companies, let say company A and company B is presented. One company (company A) produces components and the other company (company B) purchases the components to be assembled with other components to form a functional product.
Company A produces and supplies cylindrical components. The required specification of the cylinders is that the cylinders should have diameter of $(10 \pm 0.2) mm$. After producing these cylinders, the quality inspection post at company A checks the diameter of one of the produced cylinders before sending the cylinders to company B as purchaser.
From the inspection process at company A, the cylinder has diameter of $(10.3\pm 0.15) mm$.
From this inspection result, with the given mean value and the expanded uncertainty, the real diameter of the cylinder can be between $10.15mm$ and $10.45mm$. From this range, there is a probability that the real diameter of the cylinder is inside the tolerance that is $(10 \pm 0.2) mm$.
This inspection result creates a dispute!
This dispute has a very significant impact to both company as whether company A should send the part and avoid costly repair costs or company B can reject the cylinder and does not need to pay for the cylinder.
In this situation, the costs of the cylinder cannot be recovered and either company A or company B should be responsible for the cost of the cylinder production (to pay, for example, the salary of the workers of company A).
The questions are:
- What is the decision that should be made by company A from the results of the quality inspection of the cylinder with diameter of $(10.3\pm 0.15) mm$?
- Can company A send or deliver the inspected cylinder to company B as the customer?
- Can company B reject and return the cylinder to company A as the supplier?
- What should be the value of the measurement uncertainty of the cylinder so that the measurement result does not cause a dispute between company A and company B?
To answer the above questions, a tolerance diagram should be used and is explained as follow.
For this problem, the best way to solve is by using a tolerance diagram. There are two types of tolerance diagram. Both of these types have the same meaning with a difference in visualisation.
The first type of tolerance diagram is that the measurement uncertainty value is associated to the lower specification limit (LSL) and upper specification limit (USL) of a tolerance (as shown in figure 1 top and figure 2 top).
The second type of tolerance diagram is that the measurement uncertainty value is associated to a measurement result (as shown in figure 1 bottom and figure 2 bottom).
The analyses of the measured cylinder case study mentioned above are as follows.
The results of the cylinder measurement (mentioned above) lies in a dispute zone (figure 1 top). In figure 6, we can observe that, with the stated measurement uncertainty, the measured cylinder diameter has variation that cause a probability that the cylinder is actually still inside its tolerance limit.
Very often, the decision of the inspection for the given measured cylinder will be “reject”. Because, the measured diameter is above the tolerance limit of the diameter.
However, according to ISO14253-1 about decision rule to determine part conformity to its specification, the measured cylinder is still considered to be within its tolerance following the stated measurement uncertainty.
The reason is that, if the measurement is repeated, there is a possibility that the measured cylinder will be inside its tolerance limit (figure 1 bottom).
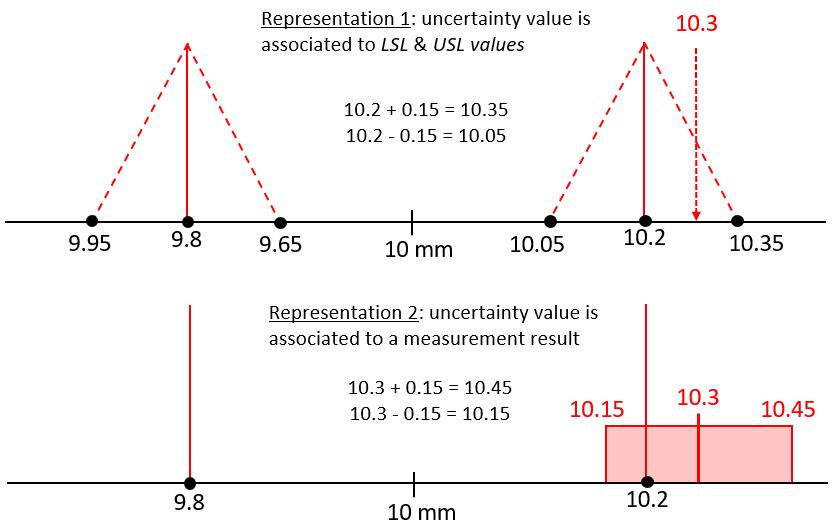
And otherwise, if the measured cylinder lies between 10.05 mm and 10.2 mm (figure 1 top). Then, the cylinder should be rejected. Because, if the measurement is repeated, there is a probability that the measurement results will be outside 10.2 mm limit.
From these situations, we can see that a large value of measurement uncertainty (low precision measurement) will cause a high probability to be in a disputed situation.
If we follow ISO14253-1, company A can send the cylinder to company B, if and only if in the buying-and-selling agreement between the two companies, the agreement did not mention a dispute situation like have been mentioned above. If there is a specific agreement between the two companies that says all components will be rejected if the components are outside their tolerance limit regardless how large their measurement uncertainty value, hence company A has to reject the cylinder.
However, company B should also understand ISO14253-1.
By following ISO14253-1, if there is no specific clause, that manages this disputed situation like has been mentioned above, in the buying-and-selling agreement between the two companies, then company B can accept the cylinder.
To avoid the disputed situation, with the given cylinder diameter tolerance of $(10 \pm 0.2) mm$ and the diameter measurement of $10.3 mm$, the measurement uncertainty should be $< 0.1 mm$.
For example, if the measurement uncertainty of the cylinder diameter is $0.05 mm$, so that the measurement result will be $(10.3\pm 0.05) mm$, then the cylinder can be confidently rejected by both company A and company B (even company A will not send the cylinder to company B). Because, the cylinder will have 95% chance to be out of its tolerance limit when the measurement is repeated (see figure 2).
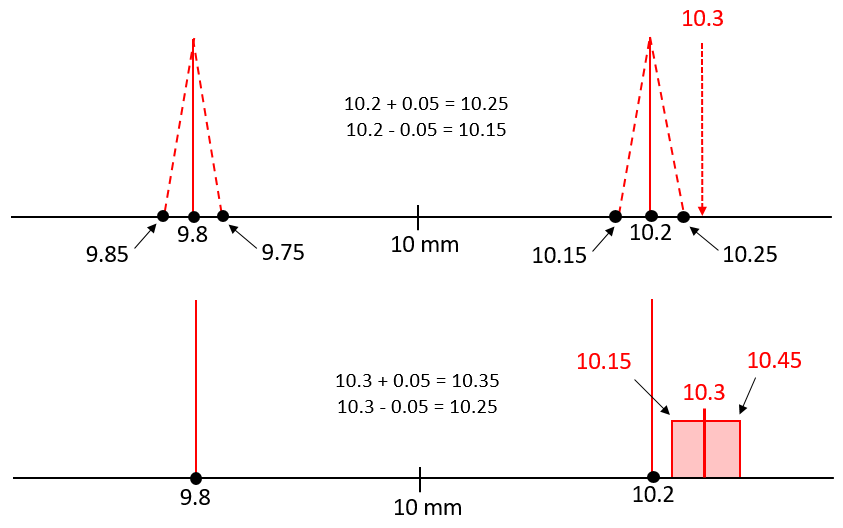
From the quantitative example presented above, we can see that the smaller the measurement uncertainty value we can get (the higher the precision of the measurement), the higher the probability we can avoid a disputing situation.
Hence, it is important to have high precision measurement by using, perhaps, a better measuring instrument. This decision of using a better measuring instrument will have an additional cost to the whole production and inspection processes.
A company should perform a trade-off analysis between the cost of involving in a disputing situation and the cost of improving its measurement capability. If the cost occurring from a disputing situation is higher than purchasing a better measuring instrument (to get high precision measurement result with small number of measurement uncertainty values), then it is worth to invest to a better measuring instrument for quality inspection.
Conclusion
In quality inspection, all decisions to determine the conformance or non-conformance of a part cannot be made unless the measurement uncertainty of the part is known.
From the given quantitively example, the critical role of measurement uncertainty in inspection processes can be understood.
In addition for a wider picture, the role of measurement uncertainty can be used to determine the capability of the inspection process in a company, whether the company should improve the measuring systems or not.
When the occurring cost due to being involved in a disputing situation is higher than the cost of purchasing a new better measuring instrument, then it is worth to invest to the new instrument to have low value of measurement uncertainties.
We sell all the source files, EXE file, include and LIB files as well as documentation of ellipse fitting by using C/C++, Qt framework, Eigen and OpenCV libraries in this link.
We sell tutorials (containing PDF files, MATLAB scripts and CAD files) about 3D tolerance stack-up analysis based on statistical method (Monte-Carlo/MC Simulation).